Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 151
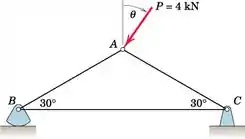
Determine e plote as forças nos três membros da treliça simples para valores de no intervalo . O que acontece se for superior a 120? Para fins de plotagem, considere as forças de tração como positivas. Determine a tração máxima e a força de compressão máxima em cada barra.
Passo 1
Uma vez que existem apenas duas forças desconhecidas agindo na junta A (dos membros AB e AC), podemos determinar ambas analisando-as.
Observe que criamos um sistema de coordenadas mOn, onde o eixo m é paralelo ao membro AC, a fim de facilitar os cálculos.
Passo 2
Observe também que assumimos que todos os membros desconhecidos estão sob tensão, portanto, os membros estarão em compressão quando seu valor for negativo.
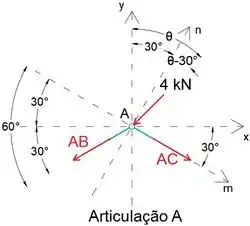
Ao igualar a soma das forças na direção n a zero, podemos determinar a torção AB
Passo 3
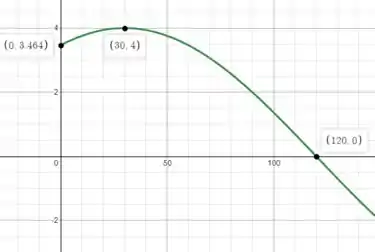
Usando uma calculadora gráfica como o Desmos (link nos comentários), vamos representar graficamente a função fornecida para AB
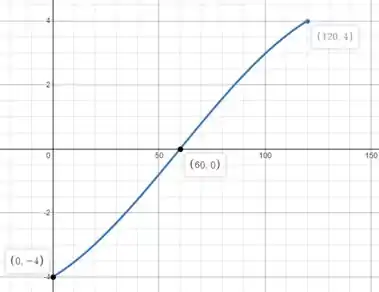
Podemos ver que a barra está em compressão (valor negativo) na faixa (), enquanto está em tensão quando , e a força de compressão máxima da barra AB é:
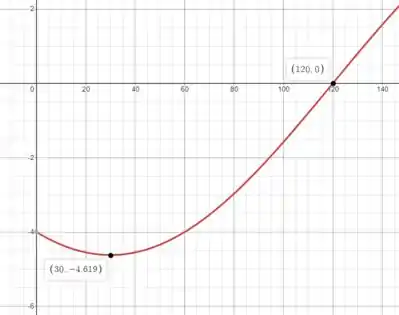
Em seguida, ao igualar a soma das forças na direção x a zero, determinaremos a força no membro AC
A partir daqui, podemos expressar AC como:
Substitua AB pela expressão (1)
Passo 4
Podemos ver que a barra está em compressão (valor negativo) na faixa (), enquanto está em tensão (valor positivo) na faixa [), e a força máxima de compressão e tensão do membro AC é:
Finalmente, vamos analisar a junta B para determinar torce no membro BC
Observe que a força de reação em B só pode agir para cima, portanto, se for negativa, a treliça irá subir.
Dito isto, a força de reação em B será negativa quando o membro AB estiver em tensão, que está em , então podemos concluir o seguinte:
Quando , a treliça subirá no ponto B.
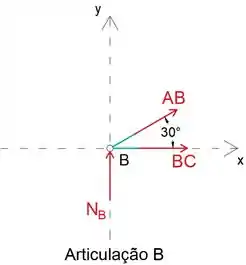
Passo 5
Ao igualar a soma das forças na direção x a zero, podemos determinar a força BC
Substitua AB pela expressão (1)
Podemos ver que a barra está em compressão (valor negativo) ao longo da faixa (), enquanto está em tensão quando , e a força de compressão máxima da barra BC é:
