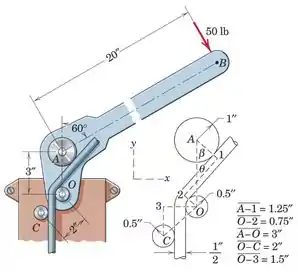
O dobrador de barra para formar aço de reforço consiste na alavanca OAB articulada em O à placa de base fixa. Os rolos formadores em A, O e C são todos livres para girar. Para a posição 60 mostrada, uma força de 50 lb é necessária na alça. Calcule os componentes x e y da força R exercida pela placa de base no eixo do rolo O para esta posição. (Sugestão: Analise diagramas de corpo livre separados da barra dobrada e da alavanca e dos roletes acoplados. Observe que a força exercida pela barra no rolete em O é adicionada à força R fornecida pela placa de base.)
Passo 1
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da barra
Observe que ângulos 302 e OA4 são iguais (ângulos com lados perpendiculares), e que a linha de ação da força de reação NO passa pelo ponto O
Usando o teorema de Pitágoras, podemos calcular a distância
Agora, usando a regra do seno, podemos calcular o ângulo
Substitua a distância por seu valor
Passo 2
Olhando para o triângulo CO3, podemos calcular o comprimento
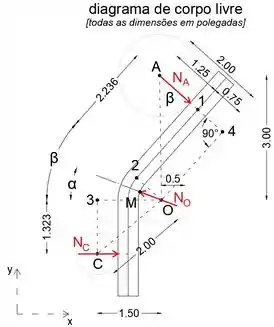
Ao igualar a soma dos momentos sobre o ponto A a zero, podemos escrever a força NC como função de NA
Ao igualar a soma das forças na direção x e y a zero, podemos determinar a escrita da força NO como função de NA
Passo 3
Substitua NC pela expressão (1) e b por seu valor
Substitua por seu valor
Dividindo as expressões (3) e (2), podemos determinar o ângulo
Passo 4
Substitua por seu valor na expressão (2) ou (3) para obter a força NO como função de NA
A seguir, vamos isolar e desenhar o diagrama de corpo livre da alavanca
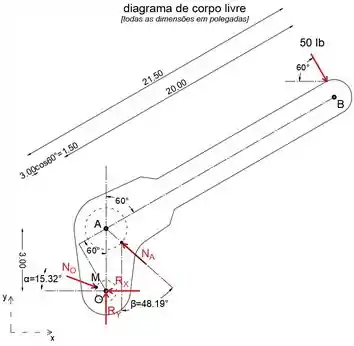
Passo 5
Ao igualar a soma dos momentos sobre o ponto O a zero, podemos determinar a força NA
Substitua NA por seu valor na expressão (4) para determinar a força NO
Finalmente, ao igualar a soma das forças na direção x e y a zero, podemos calcular as forças de reação em O
Substitua NO e NA por seus valores
Substitua NO e NA por seus valores