Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 41
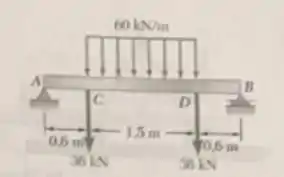
Para o carregamento na viga determine (a) os diagramas de momento fletor e cortante e (b) os valores absolutos máximos de momento fletor e esforço cortante.
Passo 1
Fala aí galera, vamos para mais um problema de estática. Para traçar os diagramas, primeiro devemos aplicar as equações de equilíbrio para determinar as reações.
Aplicando as equações, teremos:
Logo, fazendo os diagramas:
Passo 2
Como podemos ver nos diagramas, os valores máximos absolutos de momento e cortante são:
Resposta
Exercícios de Livros Relacionados
Um fio de 90m de comprimento está suspenso por dois pontos de igual elevação, que estão afastados 60m entre si. Sabendo que a tração máxima é 300N , determine (a) a flecha do fio e (b) a massa total d
Um cabo para teleférico de 200m de comprimento e massa por unidade de comprimento de 3,5k g / m é suspenso entre dois pontos de igual elevação. Sabendo que a flecha é 50m , determine (a) a distância h
Um cabo de 30m é pendurado entre dois edifícios como mostra a figura. A tensão máxima encontrada é 500N e o ponto mais baixo do cabo observado está a 4m acima do solo. Determine (a) a distância horizo
Mostre que a curva assumida por um cabo que carrega uma carga distribuída w ( x ) é definida por pela equação diferencial d 2 y / d x 2 = w ( x ) / T 0 , sendo T 0 a tração no ponto mais baixo.
Se o peso por unidade de comprimento do cabo A B é w 0 / cos 2 θ , prove que a curva formada pelo cabo é um arco de círculo. (Dica: use a propriedade indicada no Problema 7.124 ).