Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 127
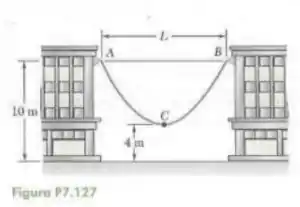
Um cabo de é pendurado entre dois edifícios como mostra a figura. A tensão máxima encontrada é e o ponto mais baixo do cabo observado está a acima do solo. Determine (a) a distância horizontal entre os edifícios, (b) a massa total do cabo.
Passo 1
Falaa, aqui a gente tem um cabo, e queremos saber a massa dele e a distância entre os prédios. Essa é uma questão para gente usar as fórmulinhas da catenária.
Bom galera, para começar, vamos fazer um diagraminha de corpo livre, só pra facilitar nossa vida:
E com isso, de cara a gente já tem alguns valores:
Repara que não vai ser direto o nosso . O é a coordenada do ponto mais baixo do cabo em relação a um sistema de referência específico (no qual a gente usa as fórmulinhas da catenária) que não necessariamente tem na linha do chão.
Mas a gente consegue perceber por essa informação que . E com isso a gente pode dizer que e achar quem é para essa situação aí, bele? Vamos lá!
Passo 2
Show de bola, aplicando a equação do livro, a gente tem =:
Aí a achamos nosso em relação àquele sistema de coordenadas específico. 😊
Agora, a equação :
Passo 3
Calma, tá quase acabando. A gente pode calcular :
E é o dobro disso, então:
Passo 4
Por fim, a gente precisa encontra a tensão máxima no cabo, pra isso vamos usar a equação :
Então, agora tá muito fácil, bora lá:
E se esse é o peso a gente pode calcular a massa: