Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 124
Mostre que a curva assumida por um cabo que carrega uma carga distribuída é definida por pela equação diferencial , sendo a tração no ponto mais baixo.
Passo 1
Bom galera, vamos começar analisando que atuam na vertical:
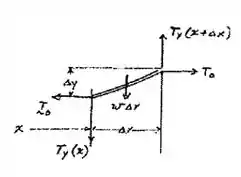
E nós sabemos que o corpo está em equilíbrio, então:
Então dividimos tudo por pra ficar parecido com o que o problema deu:
Passo 2
Show de bola, enquanto isso a gente tem que:
Então, juntando as equações, a gente encontra:
Passo 3
Por fim, a gente aplica um limite, em que :
Nós notamos que essa expressão é familiar, porque ele é aquela lá da derivada, porque é ela mesmo, logo:
Prontinho, está provado, nem é tão difícil assim vai.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Resolva o Problema 7.91 , considerando que o momento fletor que foi encontrado era + 8k N ⋅ m em D e + 9,2k N ⋅ m em E .
Resolva o Problema 7.89 , considerando que o momento fletor que foi encontrado era + 650N ⋅ m em D e + 1450N ⋅ m em E .
Sabendo que P = Q = 675N , determine a a distância a para a qual o valor absoluto máximo do momento fletor na viga A B é o menor possível, b o valor correspondenete de M m á x á . (Ver dica do Problem
Para a viga do Problema 7.47, determine (a) a razão k = P / w a para a qual o valor absoluto máximo do momento fletor na viga é o menor possível, (b) o valor corresponde |M|max. (Ver dica do Problema
Para o elemento estrutural do Problema 7.50 determine a o ângulo θ para o qual o valor absoluto máximo do momento fletor na viga A B é o menor possível, b o valor correspondente de M m á x á . (Dica: