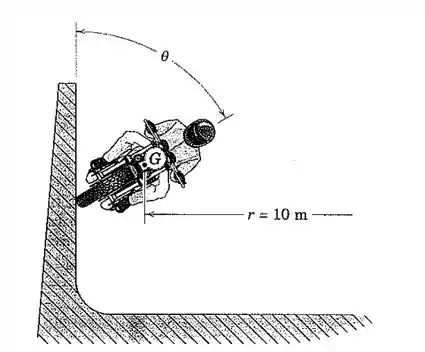
Determine a velocidade mínima e o ângulo correspondente para que a motocicleta possa andar na parede vertical de uma pista cilíndrica. O coeficiente de atrito efetivo entre os pneus e a parede é de 0,70. (note que as forças e as acelerações se encontram no plano da figura, de modo que o problema pode ser tratado como um de movimento plano com translação).

Pessoal, a primeira coisa que devemos fazer é desenhar o diagrama de corpo livre.

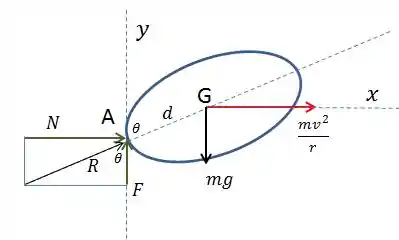
Agora vamos explicá-lo.

O ponto A é o ponto de contato entre a roda e a parede. A moto se movimenta para fora da tela, no eixo Z. Neste ponto de contato existem 2 forças atuantes: a força normal N e a força de atrito F. Usando a definição da força de atrito, temos que:

A resultante R entre as forças N e F está no eixo que passa pelo ponto de contato A e pelo centro de massa G. Disso, tiramos a relação:

Portanto, tiramos a relação:

Beleza, vamos para a o ponto G. No centro de massa do sistema atua a força peso e a força centrípeta , pois a moto está fazendo uma curva com o raio r=10m.

Agora, vamos aplicar o somatório de momentos em relação ao ponto de contato A.

Substituindo os valores: