No projeto de uma atração de parque de diversões, os carros são ligados a braços de comprimento que são articulados a um anel central rotativo que impulsiona o conjunto em torno do eixo vertical com uma velocidade angular constante . Os carros sobem e descem a pista de acordo com a relação . Encontre as componentes , e , da velocidade de cada carro quando este passa pela posição .
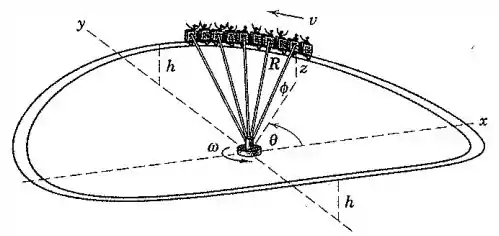
Passo 1
Vamos lembrar que as componentes da velocidade em coordenadas esféricas são dadas assim:
Como o comprimento dos braços é constante, temos:
E então, obtemos:
Passo 2
Show! Agora, para o cálculo de , já sabemos que:
Então, só falta achar . Olhando pra figura, note que:
Porém, o enunciado nos deu uma expressão de em função de :
Então, quando , teremos:
Assim, obtemos usando a relação fundamental da trigonometria:
E portanto,
Passo 3
Por último, para calcular , precisamos ainda achar , certo? Vamos utilizar as seguintes equações:
derivando-as:
Então, obtemos:
Portanto,