Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 47
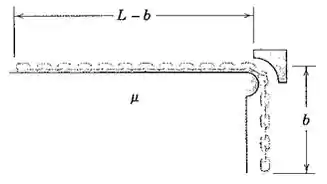
3/47) A corrente é liberada a partir do repouso com o comprimento de elos pendurados suficiente apenas para iniciar o movimento . Os coeficientes de atrito estático e dinâmico entre os elos e a superfície horizontal têm essencialmente o mesmo valor . Determine a velocidade da corrente quando o úlitmo elo passa a borda . Despreze qualquer atrito na borda .
Passo 1
Então galera , seja . Além disso , nós sabemos que a força de atrito é dada por :
Considerando que uma parte do comprimento já passou pela borda , a força normal será dada por :
Sendo assim ,
Passo 2
Analisando o conjunto de forças que atua sobre a corrente , temos que , no momento do equilíbrio :
Reparem que representa o peso da parte da corrente que já passou pela borda . Dessa forma :
Combinando (1) e (2) , achamos que :
Passo 3
Bom pessoal , assumindo que ocorra movimento , podemos fazer análise das forças que atuam na corrente através da relação :
Em que é comprimento da corrente que já passou pela borda . Nesse caso , temos que :
Agora podemos isolar na equação :
Podemos substituir e simplificar nossa expressão , obtendo que :
Resposta
De boa galera? Bora fazer mais exercícios então!