Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 52
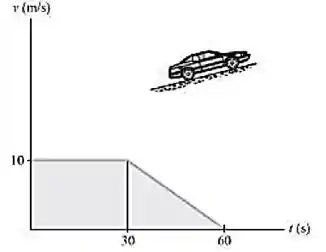
Um carro sobe uma encosta com a velocidade mostrada. Determine a distância total que o carro percorre até ele parar (t = 60s). Elabore um gráfico .
Passo 1
Sabemos que a distância percorrida é a área do gráfico . Então, calcula-se a área do retângulo e a área do triângulo e soma-se cada uma.
Assim, o deslocamento total é m.
Passo 2
Analizando o gráfico, percebe-se que, até s, a velocidade é constante, por tanto . Já em seguida, a velocidade começa à cair até zerar, de maneira linear, ou seja, aceleração constante e negativa.
Assim,
m/s²
Resposta
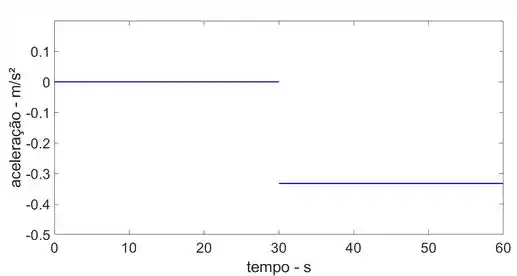
O gráfico a-t está mostrado abaixo:
Exercícios de Livros Relacionados
Quando um pequeno barco viaja para o norte a 5 km/h, uma bandeira montada na sua popa forma um ânguloθ = 50° com a linha central do barco, como mostrado na figura. Pouco depois, quando o barco está vi
Um motorista que dirige ao longo de um trecho de reta de uma rodovia diminui a velocidade de seu automóvel para uma taxa constante antes de sair da rodovia em direção a uma rampa de saída circular com
A partir de uma fotografia do dono de uma casa utilizando um removedor de neve determina-se que o raio de curvatura da trajetória da neve foi de 8,5 m a partir do momento em que ela deixa o cano de de
Um projétil é disparado a partir do ponto A com uma velocidade inicial v0. (a) Mostre que o raio de curvatura da trajetória do projétil alcança seu valor mínimo no ponto mais alto B da trajetória. (b)
Uma criança lança uma bola do ponto A com velocidade inicial vA de 20 m/s com um ângulo de 25° em relação à horizontal. Determine a velocidade da bola nos pontos da trajetória descrita pela bola onde