Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 149
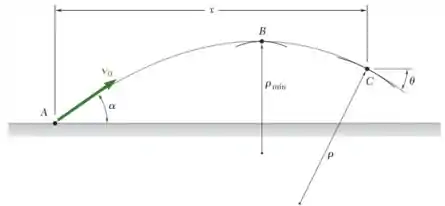
Um projétil é disparado a partir do ponto A com uma velocidade inicial v0. (a) Mostre que o raio de curvatura da trajetória do projétil alcança seu valor mínimo no ponto mais alto B da trajetória. (b) Representando por o ângulo formado entre a trajetória e a horizontal em um dado ponto C, mostre que o raio de curvatura da trajetória em C é .
Passo 1
Para o Ponto C arbitrario, nós temos
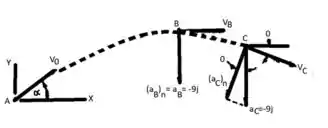
ou
Passo 2
Notando que o movimento horizontal é uniforme, nós temos
onde
Então
ou
de modo
Passo 3
(a)Ná expressão parae g são constantes, de modo que é minimo onde é maximo.
Por observação, isso ocorre no Ponto B onde .
(b)
Resposta
Exercícios de Livros Relacionados
Inicialmente, o carro move-se ao longo de uma estrada reta com uma velocidade de 35 m/s. Se os freios são aplicados e a velocidade do carro é reduzida a 10 m/s em 15 s, determine a desaceleração const
12.5. A posição da partícula é dada por s = 2 t 2 - 8 t + 6m , onde t é dado em segundos. Determine o tempo em que a velocidade da partícula é zero. Determine também a distancia total percorrida pela
Uma partícula move-se ao longo de uma linha reta com uma velocidade v = 20 - 0,05 s 2 m / s , onde s é dado em metros. Determine a aceleração da partícula em s = 15m .
Uma partícula move-se ao longo de uma linha reta com uma velocidade de v = 4 t - 3 t 2 m s , onde t é dado em segundos. Determine a posição da partícula quando t = 4s . s = 0 quando t = 0 .
Uma partícula se move ao longo de uma linha reta com uma aceleração de a = 10 - 0,2 s m / s 2 , onde s é medido em metros. Determine a velocidade da partícula quando s = 10m se v = 5m / s em s = 0 .