Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 148

Uma criança lança uma bola do ponto A com velocidade inicial vA de 20 m/s com um ângulo de 25° em relação à horizontal. Determine a velocidade da bola nos pontos da trajetória descrita pela bola onde o raio de curvatura é igual a três quartos de seu valor em A.

Passo 1

O enunciado pede que a gente determine velocidade da bola nos pontos da trajetória descrita pela bola onde o raio de curvatura é igual a três quartos de seu valor em A.

a A n = v A 2 ρ A

ρ A = v A 2 g c o s ⁡ 25 ∘

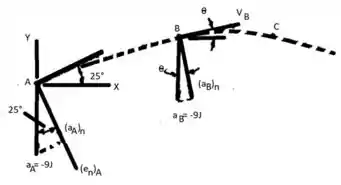
Então

ρ B = 3 4 ρ A = 3 4 v A 2 g c o s ⁡ 25 ∘

Nós temos

a B n = v B 2 ρ B

Onde

a B n = g c o s ⁡ θ

para isso 3 4 v A 2 g c o s ⁡ 25 ∘ = v B 2 g c o s ⁡ θ

ou

(1)

v B 2 = 3 4 cos ⁡ θ cos ⁡ 25 ∘ v A 2

Passo 2

Notando que o movimento horizontal é uniforme, nós temos

v A x = v B x

onde

v A x = v A c o s ⁡ 25 ∘ v B x = v B c o s ⁡ θ

Então

v A c o s ⁡ 25 ∘ = v B c o s ⁡ θ

ou

c o s ⁡ θ = v A v B c o s ⁡ 25 ∘

Substituindo para cos θ na EQ. (1), nós temos

v B 2 = 3 4 v A v B c o s ⁡ 25 ∘ v A 2 cos ⁡ 25 ∘

ou

v B 3 = 3 4 v A 3

v B = 3 4 3 v A = 18.17 m / s

c o s ⁡ θ & = 4 3 3 c o s ⁡ 25 ∘

θ & = ± 4.04 ∘

v B = 18.17 m / s     ∡   4.04 ∘ v B = 18.17 m / s     ∡   4.04 ∘

Resposta

v B = 18.17 m / s     ∡   4.04 ∘ v B = 18.17 m / s     ∡   4.04 ∘

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A aceleração de uma partícula se movendo ao longo de uma linha reta é a = k / v , onde k é uma constante. Se s = 0 , v = v 0 quando t = 0 , determine a velocidade da partícula como uma função do tempo
Um carro está se movendo a 15m / s , quando um semáforo, 50m à sua frente, acende a luz amarela. Determine a desaceleração constante exigida do carro e o tempo necessário para parar no semáforo.
Uma bola é solta da parte de baixo de um elevador que está se movendo para cima com uma velocidade de 2 m/s. Se a bola bate no fundo do poço do elevador em 3 s, determine a altura do elevador a partir
Se uma partícula tem uma velocidade inicial de v 0 = 12m / s para a direita, em s 0 = 0 , determine a sua posição quando t = 10s , se a = 2m / s 2 para a esquerda.
Um trem parte do repouso em uma estação e move-se com uma aceleração constante de 1m / s 2 . Determine a velocidade do trem quando t = 30s e a distância percorrida durante este tempo.