Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 144
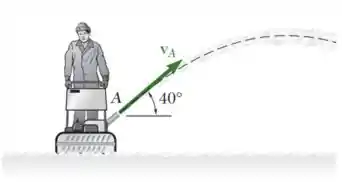
A partir de uma fotografia do dono de uma casa utilizando um removedor de neve determina-se que o raio de curvatura da trajetória da neve foi de 8,5 m a partir do momento em que ela deixa o cano de descarga em A. Determine (a) a velocidade de descarga vA da neve, (b) o raio de curvatura no ponto mais alto da trajetória.
Passo 1
(a)Nós temos
ou
ou
Passo 2
(b)Nós temos
Onde o Ponto B é o ponto mais alto da tragetória, dito isso
Então
ou
Resposta
Exercícios de Livros Relacionados
3/45) os cursores A e B são conectados por uma barra leve rígida e se deslocam com atrito despresível nos rasgos , ambos se encontram em um plano horizontal. Para a posição mostrada , a velocidade de
Repita o Prob. 2/56, porém agora inclua os efeitos do arrasto aerodinâmico. As forças de arrasto provocam uma componente de aceleração em m / s 2 de 0,016 v 2 na direção oposta ao vetor velocidade, on
Uma bola é jogada verticalmente para cima com uma velocidade de 15 m/s. Determine o tempo do voo quando ela retorna para sua posição original.
Uma partícula move-se ao longo de uma linha reta com uma velocidade de v = 0,5 t 3 - 8 tm / s , onde t é dado em segundos. Determine a aceleração da partícula quando t = 2s .
Uma partícula move-se ao longo de uma linha reta de maneira que a sua aceleração é a = 4 t 2 - 2m / s 2 , onde t é dado em segundos. Quando t = 0 , a partícula está localizada 2 m à esquerda da origem