Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 130
Quando um pequeno barco viaja para o norte a 5 km/h, uma bandeira montada na sua popa forma um ângulo = 50° com a linha central do barco, como mostrado na figura. Pouco depois, quando o barco está viajando para leste a 20 km/h, o ângulo é novamente de 50°. Determine a velocidade escalar e a direção do vento.
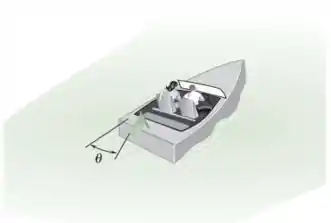
Passo 1
Nós temos
Usando essa equação, os dois casos são representados graficamente abaixo.
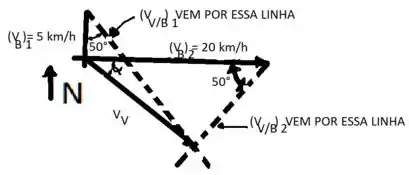
Com agora definido, o diagrama abaixo é redesenhado para clarificar os dois casos.
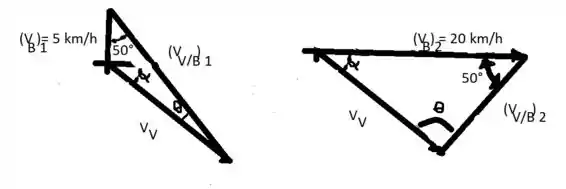
Notando que
Nós temos
Portanto
ou
ou
ou
Então
Resposta
Exercícios de Livros Relacionados
Um trem de metrô com três vagões está percorrendo uma descida com 5 % de inclinação quando os freios individuais dos vagões são acionados simultaneamente. Cada vagão de 10t pode gerar uma força de fre
3/42) Se a esfera de aço do Prob. 3/41 é liberada a partir do repouso na superfície de um líquido no qual a resistência ao movimento é R = c v 2 , onde c é uma constante e v é a velocidade da esfera p
3/43) Determine a faixa de variação da força aplicada P para a qual o bloco de massa m 2 não escorregará sobre o bloco em formato de cunha de massa m 1 . Despreze o atrito associado com as rodas do bl
3/46) Duas esferas de ferro , cada uma das quais com 100m m de diâmetro , são liberadas a partir do repouso com uma separação de centro de 1m . Suponha um lugar no espaço sem nenhuma força , além da f
3/44) Os cursores A e B estão conectados por uma barra leve rígida de comprimento l = 0,5m e se deslocam com atrito desprezível nos rasgos horizontais mostrados . Para a posição onde x A = 0,4m , a ve