Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 52

Um carro está viajando em uma estrada com inclinação lateral a uma velocidade constante v. Determine o intervalo de valores de v para os quais o carro não derrapa. Expresse sua resposta em termos do raio r da curva, do ângulo de inclinação da estrada e do ângulo de atrito estáticos entre os pneus e o pavimento.

Passo 1

E ai gurizada tudo beleza? O enunciado pede que a gente expresse a resposta em termos do raio r da curva, do ângulo de inclinação da estrada e do ângulo de atrito estáticos entre os pneus e o pavimento.

Vaoms considerar 2 situações para decompormos a força, venham comigo :D

Passo 2

1º caso: Considere a inclinação do carro a seguir:

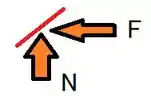
v = vmax

Nota: R = F+N

+ ∑ F n = m a n :         R sin ⁡ θ + ϕ s = m v m a x 2 r                             ( 1 ) + Σ ^ F y = 0 :         R c o s ⁡ θ + ϕ s - W = 0         R cos ⁡ θ + ϕ s = m g                                           ( 2 )

Ou

Formando (1)/(2) Rsin ⁡ θ + ϕ s Rcos ⁡ θ + ϕ s = m - v m a x 2 r m g o u v m a x = g r t a n ⁡ θ + ϕ s

Passo 3

2º caso: Considere a inclinação do carro a seguir:

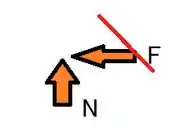
v = v min

Nota : R = F+N

+ Σ F n = m a n : R sin ⁡ θ - ϕ s = m v m i n 2 r                       ( 3 ) + † Σ F y = 0 : R c o s ⁡ θ - ϕ s - W = 0 R cos ⁡ θ - ϕ s = m g                                                                                   ( 4 )

Ou

Formando (3)/(4) Rsin ⁡ θ - ϕ N Rcos ⁡ θ - ϕ s = m v m i n 2 r m g o u v m i n = grtan ⁡ θ - ϕ s

para o carro não derrapar g r t a n ⁡ θ - ϕ s ≦ v ≤ g r t a n ⁡ θ + ϕ s

Resposta

g r t a n ⁡ θ - ϕ s ≦ v ≤ g r t a n ⁡ θ + ϕ s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O guincho transmite uma força de reboque horizontal F ao seu cabo em A , que varia como mostrado no gráfico. Determine a velocidade do balde de 8 0k g quando t = 24s . Originalmente o balde é solto do
O trem consiste de uma locomotiva E de 30M g e dos vagões A ,B e C , que têm massas de 15M g , 10M g e 8M g , respectivamente. Se os trilhos proporcionam uma força de tração de F = 30k N às rodas da l
O guincho transmite uma força de reboque horizontal F ao seu cabo em A , que varia como mostrado no gráfico. Determine a velocidade do balde de 70k g quando t = 18s . Originalmente o balde está se mov
No instante em que se rompe o cabo, a caixa de 100k g está subindo pelo plano a uma velocidade de 4,5m / s . Determine a velocidade da caixa 2 segundos depois. O coeficiente de atrito cinético entre a
O motor M puxa o cabo com uma força F , que tem uma intensidade que varia conforme mostra o gráfico. Se a caixa de 20k g está originalmente em repouso no solo, de modo que a tração do cabo seja zero n