Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 22
No instante em que se rompe o cabo, a caixa de está subindo pelo plano a uma velocidade de . Determine a velocidade da caixa segundos depois. O coeficiente de atrito cinético entre a caixa e o plano é .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Bom... Para este problema temos a seguinte situação... Quando o cabo se rompe caixa continua subindo, então para e depois começa a descer, concorda?
Vamos fazer o diagrama do corpo livre do sistema na subida. Temos:
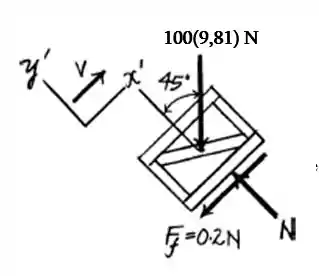
Analisando em temos:
Assim a força de atrito será
E aí que vem o detalhe importante do problema: a força de atrito é contrária ao movimento da caixa, então quando a caixa estiver subindo essa força apontará na direção e quando a caixa estiver descendo a força apontará no sentido .
Passo 2
Então a nossa estratégia vai ser o seguinte: como queremos saber a velocidade do corpo após o rompimento do cabo, primeiro temos que saber se esse corpo está subindo ainda ou já está descendo. Pra isso vamos olhar primeiro a subida, beleza?
Na subida a força resultante sobre o bloco será
E a aceleração sobre ele é
Assim escrevendo a equação para velocidade desse bloco
E essa equação só é válida para por que enquanto o bloco sobre a nossa aceleração será essa! Quando o bloco estiver descendo a aceleração resultante será outra
Vamos ver se o bloco termina o seu movimento de subida antes dos . Pra isso vamos fazer
Então depois de da corda ter rompido o bloco estará descendo! Então temos que olhar esse movimento agora.
Passo 3
Na descida a força resultante será
Que nos dá a seguinte aceleração
Assim o nosso segundo movimento será
Nesse segundo movimento a velocidade inicial será nula (quando o bloco atingiu altura máxima), então
Aqui corresponde ao instante em que o bloco atinge altura máxima. Assim o instante que corresponde a depois da corda ter se rompido é . Jogando na nossa equaçãozinha
Feshow!