Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 114
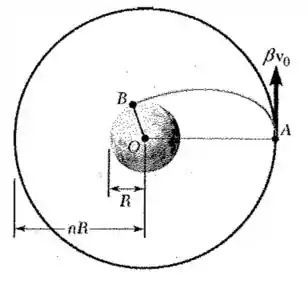
Uma sonda espacial está descrevendo uma órbita circular de raio nR com uma velocidade escalar v0 ao redor de um planeta de raio R e centro O. Quando ela passa pelo ponto A, sua velocidade escalar é reduzida de v0 para onde , para ser inserida em uma trajetória de impacto. Expresse em termos de n e o ângulo AOB, onde B representa o ponto de impacto da sonda sobre o planeta.
Passo 1
Essa questão pede que a gente expresse em termos de n e o ângulo AOB, onde B representa o ponto de impacto da sonda sobre o planeta. Consideraremos os seguintes dados
Para órbita circular,
A tragetória de colisão é eliptica.
Passo 2
Ao ponto A,
Ao ponto de impacto B,
Resposta
Exercícios de Livros Relacionados
Uma partícula de 2 kg desloca-se ao longo de uma trajetória definida por r = 3 + 2 t 2m , θ = 1 3 t 3 + 2r a d E z = ( 5 - 2 t 2 ) m, onde t é dado em segundos. Determine as componentes da força r , θ
Determine a intensidade da força resultante atuando sobre uma partícula de 5 kg no instante t = 2 s, se a partícula está se movendo ao longo de uma trajetória horizontal definida pelas equações r = (
Se o coeficiente de atrito estático entre o bloco de massa m e a plataforma giratória é μ s , determine a velocidade angular constante máxima da plataforma que não faça com que o bloco escorregue.
A trajetória do movimento de uma partícula de 5 kg no plano horizontal é descrita em termos das coordenadas polares como r = ( 2 t + 1 ) m e θ = ( 0,5 t 2 - t ) , onde t é dado em segundo. Determine a
Partindo do repouso, uma lancha move-se em torno de uma trajetória circular, ρ = 50m , a uma velocidade escalar v = 0,2t 2m / s , onde t é dado em segundos. Determine as intensidades da velocidade e a