Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 24
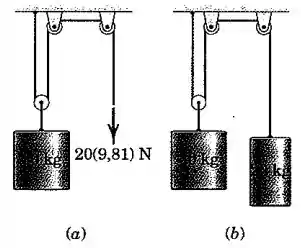
Determine a aceleração vertical do cilindro de para cada um dos dois casos. Despreze o atrito e a massa das polias.
Passo 1
(a) Temos uma tração ao longo da corda, o que significa que o cilindro é puxado para cima com uma força , enquanto seu peso o puxa para baixo. Pela Segunda Lei de Newton:
Passo 2
(b) Nesse caso, um outro cilindro, de , é adicionado na ponta da corda. Considere a tração ao longo da corda e a aceleração desse cilindro. Vamos aplicar a Segunda Lei de Newton a ele:
Também aplicamos a Segunda Lei de Newton ao cilindro de :
Passo 3
Por enquanto, chegamos a duas equações, mas com três incógnitas, a saber: , e . O que podemos fazer é achar uma equação que relacione as acelerações dos dois cilindros.
Seja a distância entre a polia móvel (presa ao cilindro de ) e a polia fixa no teto, logo acima dela, e a distância entre o bloco de e a polia fixa no teto, logo acima dele. Então o comprimento total da corda é:
Como o comprimento é constante, se derivarmos duas vezes essa equação em relação ao tempo, obteremos:
Ou seja,
Agora sim temos três equações e três incógnitas, e podemos resolver o sistema:
cuja solução é:
Resposta
(a)
(b)