Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 23
Se os coeficientes de atrito estático e dinâmico entre o bloco de e o carrinho de têm ambos essencialmente o mesmo valor de , determine a aceleração de cada parte para
(a) e
(b) .
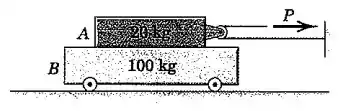
Passo 1
(a) Para saber se há deslizamento entre os blocos, primeiramente vamos calcular a força de atrito estático máxima:
A corda que puxa o bloco passa por uma roldana, então já sabemos que é puxado para a direita com uma força . Porém, aí surge uma tendência de movimento desse bloco para a direita, e aí a força de atrito estático age para a esquerda, tentando coibir o movimento. Porém, como acabamos de calcular, a força de atrito estático máxima é , enquanto a outra força é de , o que significa que o bloco pode acabar entrando em movimento.
Então, passaria a agir a força de atrito dinâmico, calculada da mesma forma:
As forças de atrito estático e dinâmico só coincidiram porque os coeficientes de atrito eram iguais.
Passo 2
Assumindo então que há deslizamento, aplicamos a Segunda Lei de Newton ao bloco :
A força de atrito que calculamos é exercida pela superfície do bloco sobre o bloco , para a esquerda, para opor-se ao movimento de . No entanto, toda força de ação tem uma força de reação, igual em módulo e atuando em sentido contrário. Então, a força de atrito que calculamos também age em , só que para a direita.
Sabendo disto, aplicamos a Segunda Lei de Newton ao bloco :
Como , realmente houve deslizamento.
Passo 3
(b) Para , teremos a força atuando em para a direita. Porém, como já calculamos, a força de atrito estático máxima é , o que significa que a força de atrito estático pode compensar a outra força, a ponto de não permitir que os blocos deslizem entre si.
Sendo assim, os blocos poderiam se locomover, mas grudados um no outro, sem deslizamento. Então poderíamos tratá-los matematicamente como apenas um grande bloco , de massa , e a única força externa agindo sobre ele seria .
Vamos então aplicar a Segunda Lei de Newton a esse fictício, mas bastante útil bloco :
Ou seja, teremos:
Resposta
(a)
(b)