Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 22
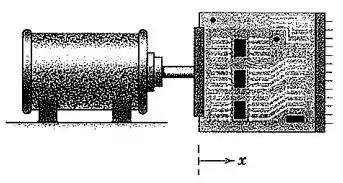
Durante um teste de confiabilidade, uma placa de circuito impresso de massa é fixada a um shaker eletromagnético e submetida a um deslocamento harmônico , onde é a amplitude do movimento, é a frequência do movimento em radianos por segundo, e é o tempo. Determine o módulo da força horizontal máxima que o shaker exerce sobre a placa de circuito impresso.
Passo 1
Pessoal, se derivarmos a expressão do deslocamento em relação ao tempo, obteremos a velocidade:
Derivando mais uma vez, obtemos a aceleração:
Passo 2
Usando a Segunda Lei de Newton, achamos a força horizontal que o shaker exerce sobre a placa de circuito:
Como , o módulo da força máxima será:
Resposta
Exercícios de Livros Relacionados
Um policial motociclista parte do repouso em A dois segundos depois que um carro, correndo a uma velocidade constante de 120k m / h , passa pelo ponto A . Se o patrulheiro acelera a uma taxa de 6m / s
O cone caindo com uma velocidade v 0 atinge e penetra o bloco de material de embalagem . A aceleração do cone após o impacto é a = g - c y ² ², onde c é uma constante positiva e y é a distância de pen
Um pequeno objeto é liberado a partir do repouso em um tanque de óleo. A aceleração de descida do objeto é g - k v , onde g é a aceleração constante devido à gravidade, k é uma constante que depende d
Uma cápsula impulsionada a vácuo para um sistema de transporte tubular de alta velocidade do futuro está sendo projetada para operação entre duas estações A e B , que estão distantes 10k m . Se a acel
A resistência aerodinâmica ao movimento de um carro é aproximadamente proporcional ao quadrado da sua velocidade. A resistência adicional ao atrito é constante, de modo que a aceleração do carro quand