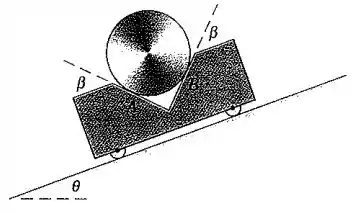
Um cilindro de massa repousa em um carro de suporte como mostrado. Se e , calcule a máxima aceleração que o carro pode receber para cima do plano inclinado de modo que o cilindro não perca o contato em .

Galera, a principal sacada aqui é perceber que, quando o cilindro perde o contato em , a força normal nesse ponto é nula, então a única normal agindo seria em , vamos dizer . Como queremos o caso-limite, podemos considerar .

Como este é um problema de plano inclinado, é melhor considerar o eixo como a direção da inclinação de , e o eixo como perpendicular a este. Sendo assim, as forças na “vertical” serão , uma componente da força peso, e , uma componente da normal em .

Talvez pareça estranho que a normal tenha apenas uma componente na direção , pois geralmente em problemas de plano inclinado essas forças aparecem com direção igual ao do eixo . Mas nesses problemas, as superfícies dos corpos em questão seguem a mesma inclinação do plano inclinado, e aqui não. A normal sempre tem que ser perpendicular à superfície, o que faz com que no nosso problema, os valores da normal dependam do ângulo .

Como estamos considerando não haver movimento na “vertical”, as forças se anulam: