Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 146

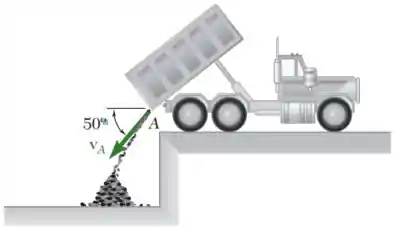
O carvão é descarregado da carroceria de um caminhão basculante com uma velocidade inicial de vA = 2 m/s ∡ 50°. Determine o raio de curvatura da trajetória descrita pelo carvão (a) no ponto A, (b) no ponto da trajetória localizado 1 m abaixo do ponto A.

Passo 1

(a)Nós temos o diagrama esboçando o caminhão a seguir

a A n = v A 2 ρ A

ρ A = ( 2 m / s ) 2 9,81   m / s 2 c o s ⁡ 50 ∘

ρ A = 0,63   m

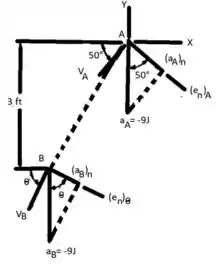
Passo 2

(b)Movimento Horizontal. (Uniforme)

v B x = v A x = ( 2   m / s ) c o s ⁡ 50 ∘ = 1,285   m / s

Movimento Vertical. (Movimento Uniformemente Acelerado)

Nós temos

v y 2 = v A y 2 - 2 g y - y A 0 g = 9,81   m / s 2

onde

v A y = ( 2   m / s ) s i n ⁡ 50 ∘ = 1,53   m / s

No Ponto B, y = -3 ft:

v b y 2 = ( 1,53 ) 2 - 2 9,81 ( - 1 )

ou

v B y = 1 7,27   m / s

Então

v B = v B x 2 + v B y 2 = ( 1,285 ) 2 + ( 17,27 ) 2 = 17,31   m / s

e

t a n ⁡ θ = v y v x = 17,27 1,285

ou θ = 85,74 °

Agora

a B n = v B 2 ρ B

ρ B = ( 1 7,31   m / s ) 2 9,81 / s 2 c o s ⁡ 85,7 4 ∘

ρ B = 411,86   m

Resposta

ρ A = 0,63   m

ρ B = 411,86   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O gráfico s-t para um trem foi determinado experimentalmente. A partir dos dados, construa os gráficos v-t e a-t para o movimento.
Um barco move-se em uma linha reta com a aceleração descrita pelo gráfico a-s. Se ele parte do repouso, construa o gráfico v-s e determine a velocidade escalar máxima do barco. Que distância s’ ele pe
Um foguete tem uma aceleração descrita pelo gráfico. Se ele parte do repouso, construa os gráficos v-t e s-t para o movimento no intervalo de tempo 0
A partícula move-se ao longo de uma linha reta com a velocidade descrita pelo gráfico. Construa o gráfico a - s .
Um trem parte da estação A e no, percurso do primeiro quilômetro, ele move-se com aceleração uniforme. Então, pelos próximos 2 quilômetros, move-se com velocidade escalar uniforme. Por fim, o trem des