Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 148

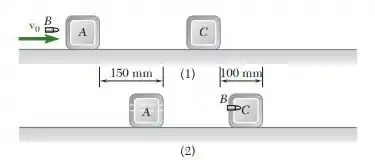
A bala B tem massa de 15 g e os blocos A e C de 1,5 kg. O coeficiente de atrito entre os blocos e o plano μ k = 0,25. Inicialmente a bala está se movendo em v 0 e os blocos A e C estão em repouso (Figura 1). Depois que a bala passa por meio de A, ela penetra em C e todos os três objetos param na posição mostrada na figura (Figura 2). Determine a velocidade inicial da bala v 0 .

Passo 1

Esta questão não é complicada, mas dá um certo trabalho em ser feita. Neste caso, a bala B, com certa velocidade inicial, passa pelo bloco A e penetra no bloco C. O bloco A desliza após a passagem da bala e o bloco C também desliza após a penetração da bala. Então vamos estabelecer o seguinte:

  • v 0 é a velocidade inicial da bala;
  • v 1 é a velocidade da bala depois que atravessa o bloco A;
  • v A é a velocidade do bloco A imediatamente após a passagem da bala;
  • v C é a velocidade do bloco C junto com a bala.

Usando a conservação de quantidade de movimento, podemos relacionar a v 0 , v 1 e v A

m B v 0 + m A v A 0 = m B v 1 + m A v A → v A 0 = 0

v 0 = v 1 + m A v A m B

Para o bloco C, temos:

m B v 1 + m C v C 0 = ( m B + m C ) → v C 0 = 0

v 1 = m B + m C v C m B

Passo 2

Agora precisamos determinar as velocidades dos blocos A e C quando deslizam. Para isso vamos usar o princípio de trabalho e energia. Para o bloco A:

T 1 + U 1 → 2 = T 2

1 2 m A v A 2 - μ k N A d A = 0 → v A =   2 μ k m A g d A m A =   2 μ k g d A

v A = 2 0,25 9,81 0,15 = 0,858   m / s

Para o bloco C:

1 2 m B + m C v C 2 - μ k m B + m C g d C = 0 → v C = 2 μ k g d C

v C =   2 0,25 9,81 0,1 = 0,700   m / s

Passo 3

Como temos os valores de v A e v C , podemos obter v 1 e v 0 . Assim:

v 1 = 1,5 + 0,015 0,700 0,015 =   70,7   m / s

Logo, a velocidade inicial da bala é:

v 0 = 70,7 + 1,5 ⋅ 0,858 0,015 = 156,5   m / s

Resposta

v 0 = 156,5   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um automóvel de 1.200k g está movendo a uma velocidade 90k m / h quando os freios são totalmente aplicados, causando o escorregamento de todas as quatro rodas. Determine o tempo necessário para parar
Um colar de 2 kg pode deslizar sobre uma barra vertical sem atrito e está sujeito a uma força P cuja intensidade varia como mostrado na figura. Sabendo que o colar está inicialmente em repouso, determ
Um cilindro C de 8 kg repousa sobre uma plataforma A de 4 kg sustentada por uma corda que passa sobre as roldanas D e E e é presa a um bloco B de 4 kg. Sabendo que o sistema é liberado do repouso, det
O sistema mostrado na figura é liberado do repouso. Determine o tempo necessário para a velocidade de A atingir 1 m/s. Despreze o atrito e a massa das roldanas.
Um colar de 2 kg pode deslizar sobre uma barra vertical sem atrito e está sujeito a uma força P cuja intensidade varia como mostrado na figura. Sabendo que o colar está inicialmente em repouso, determ