Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 74
O helicóptero mostrado na figura consegue produzir uma velocidade de ar descendente máxima de 25 m/s em uma corrente de ar de 10 m de diâmetro. Sabendo que o peso do helicóptero e da tripulação é de 18 kN e considerando = 1,21 kg/m3 para o ar, determine a carga máxima que o helicóptero pode erguer quando paira.
Passo 1
Essa questão é bem legal. Para determinar a carga máxima que o helicóptero, primeiro vamos calcular o máximo empuxo que a vazão de ar que passa pelas pás. O movimento das pás gera um volume de ar descendente. Assim, vamos assumir que esse volume de ar é igual ao volume de um cilindro como mostrado na figura abaixo:
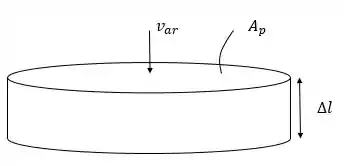
Logo, a o empuxo produzido por essa corrente de ar é dada por:
Passo 2
Analisando a equação do passo 1, temos que dm/dt representa a taxa de variação de massa dentro desse cilindro imaginário, em que é permitido que massa entre ou saia dele. Podemos calcular a variação de massa através de:
Onde é a área formada pelas pás do helicóptero em movimento. Dividindo ambos os lados por :
A velocidade das partículas de ar acima das pás é considerada nula. Com isso, . Substituindo tudo na equação do passo 1:
O sentido da força aponta para cima.
Passo 3
Agora para calcular a carga máxima, vamos admitir que quando o helicóptero paira no ar, ele está em repouso em relação a um observador no solo. Com isso, fazemos um somatório de forças em y: