Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 63
Um foguete tem uma aceleração descrita pelo gráfico. Se ele parte do repouso, construa os gráficos v-t e s-t para o movimento no intervalo de tempo 0
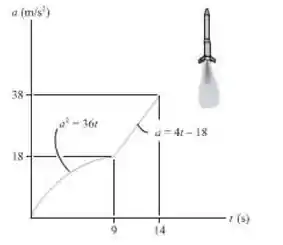
Passo 1
Gráfico v-t:
Para 0
Quando t = 9 s,
A condição inicial é v = 108 m/s em t = 9s,
Quando t = 14 s,
Passo 2
Gráfico s-t:
Para o intervalo 0
Quando t = 9s,
Para o intervalo de tempo 9
Quando t = 14s,
Resposta
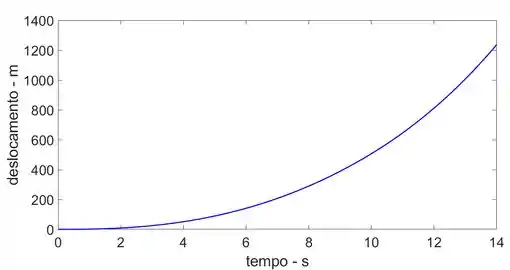
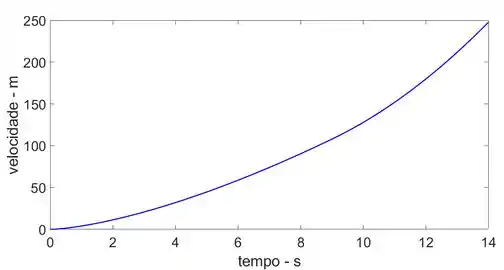
O gráfico s-t e v-t estão representados abaixo,
Exercícios de Livros Relacionados
Dois satélites A e B percorrerem órbitas circulares coplanares em torno da Terra com altitudes de 190 e 320 km, respectivamente. Se em t = 0 os satélites estão alinhados como mostrado na figura e sabe
Considere uma partícula de massa m cujo movimento inicia a partir do repouso em um campo gravitacional constante. Se uma força resistiva proporcional ao quadrado da velocidade (isto é, k m v 2 ) for e
Uma partícula é lançada verticalmente para cima em um campo gravitacional constante com velocidade inicial v 0 . Demonstre que se existir uma força de retardo proporcional ao quadrado da velocidade in
Repita o Exemplo 2.4 efetuando um cálculo no computador para resolver a equação 2.22. Use os valores a seguir: m = 1 k g , v 0 = 10 m / s , x 0 = 0 e k = 0,1 s - 1 . Elabore gráficos de v versus t , x
Uma partícula de massa m desliza para baixo sobre um plano inclinado sob a influência da gravidade. Se o movimento estiver sujeito a uma força resistiva f = k m v 2 , demonstre que o tempo necessário