Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 47
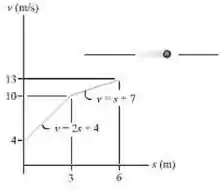
A partícula move-se ao longo de uma linha reta com a velocidade descrita pelo gráfico. Construa o gráfico .
Passo 1
Sabemos que, quando o gráfico é conhecido, a aceleração em qualquer posição pode ser determinada utilizando,
Reescrevendo,
Passo 2
Observando o gráfico, vemos que há 2 comportamentos diferentes, de 0 à 3 m e de 0 à 6 m.
Assim, aplicando ao nosso problema, para cada comportamento,
Para ,
Para ,
Passo 3
Agora vamos calcular o valor de nos extremos, ou seja, em , e m.
Para ,
Para ,
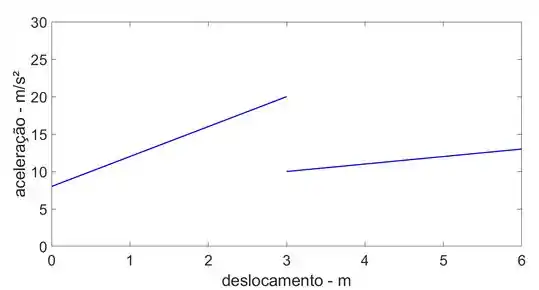
Resposta
O gráfico está mostrado abaixo.
Exercícios de Livros Relacionados
A velocidade de uma partícula que se desloca em linha reta está diminuindo, a uma taxa de 3m / s por metro de deslocamento, em um instante quando a velocidade é de 10m / s . Determine a aceleração a d
Um carro para completamente a partir de uma velocidade inicial de 80k m / h em uma distância de 30m . Com a mesma aceleração constante, qual seria a distância s de parada a partir de uma velocidade in
Um foguete é disparado verticalmente para cima do repouso. Se este foi projetado para manter uma aceleração constante para cima de 1,5 g , calcule o tempo t necessário para alcançar uma altitude de 30
Considere um projétil disparado verticalmente em um campo gravitacional constante. Para as mesmas velocidades iniciais, compare os tempos necessários para que o projétil alcance sua altura máxima (a)
Uma partícula de massa m = 1k g está sujeita a uma força unidimensional F t = k t e - α t , onde k = 1 N s e α = 0,5s - 1 . Se a partícula estiver inicialmente em repouso, calcule e elabore um gráfico