Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 67
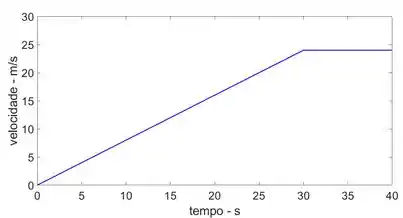
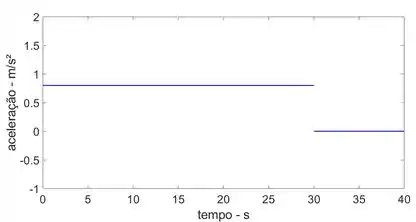
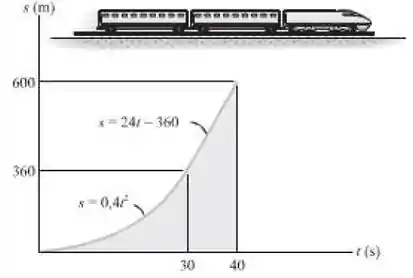
O gráfico s-t para um trem foi determinado experimentalmente. A partir dos dados, construa os gráficos v-t e a-t para o movimento.
Passo 1
Avaliando-se o gráfico de posição vs tempo, percebe-se que há duas curvas diferentes caracterizando esse deslocamento. Como se sabe, a velocidade é equivalente a primeira derivada da função de posição s(t) e a aceleração é equivalente a segunda derivada da função s(t). Deste modo, serão realizadas tais operações, de acordo com a faixa de tempo para cada função.
Passo 2
Para 0 ≤ t ≤ 30, a função s(t) = 0,4t² m
Para 30 ≤ t ≤ 40, a função s(t) = (24t – 360) m
Derivando as funções, temos que a função de velocidade é:
Para 0 ≤ t ≤ 30, a função v(t) = 0,8t m/s
Para 30 ≤ t ≤ 40, a função v(t) = 24 m/s
Seguindo os passos, a função de aceleração é dada por:
Para 0 ≤ t ≤ 30, a função v(t) = 0,8 m/s²
Para 30 ≤ t ≤ 40, a função v(t) = 0 m/s²
Resposta
Os gráficos v-t e a-t estão mostrados abaixo:
