Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 2

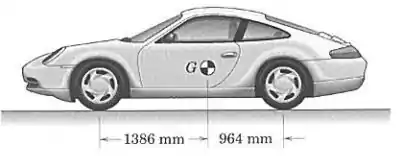
O centro de massa do carro de motor traseiro e com está localizado como mostrado na figura. Determine a força normal sob cada pneu quando o carro está em equilíbrio. Descreva qualquer hipótese feita.

Passo 1

Galera, vamos considerar a hipótese de que o carro tem simetria entre suas partes direita e esquerda, de modo que o centro de massa fica à mesma distância entre as rodas direita e esquerda, seja as da frente ou as de trás.

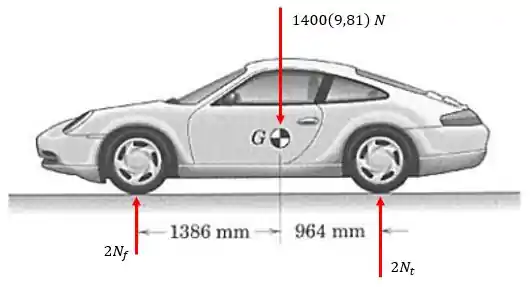
Sendo assim, podemos tratar o problema como bidimensional, e fazer o diagrama de forças sobre o carro desse modo:

Passo 2

Para que haja equilíbrio, devemos ter uma resultante de forças nula (vertical):

Além disso, o somatório dos momentos também deve ser nulo (em relação à roda da frente):

Voltando na equação de equilíbro das forças, determinamos a normal :

Resposta

(pneus da frente)

(pneus de trás)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um procedimento para avaliar a resistência do músculo tríceps, uma pessoa força para baixo uma célula de carga com a palma da mão, como mostrado na figura. Se a leitura da célula de carga é de 160N

O conector de correntes é utilizado para segurar cargas de troncos, madeira, tubos e congêneres. Se a força trativa T 1 vale 2k N quando θ = 30 ° , determine a força P necessária na alavanca e a força

O dispositivo mostrado é projetado para aplicar pressão dos dois lados de uma bancada, durante a colagem do laminado próximo à borda. Se uma força de 120N é aplicada à barra, determine a força que cad

Para comprovar a validade das hipóteses aerodinâmicas feitas no projeto de um avião, seu modelo está sendo testado em um túnel de vento. O suporte está conectado a um dispositivo para equilibrar força

As duas polias leves são presas uma à outra e formam uma unidade única. Elas são impedidas de girar em torno de seu mancal em O por um cabo enrolado firmemente em torno da polia menor e preso ao ponto