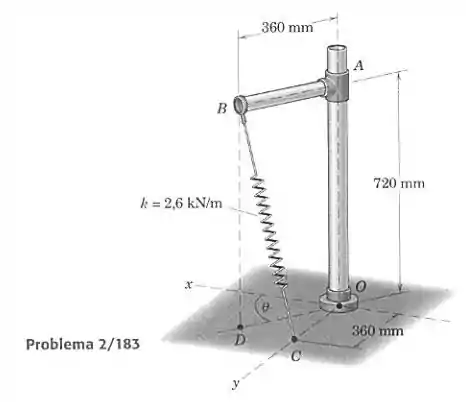
O braço gira na faixa , e a mola não está esticada quando . Determine, em função de , o momento em torno de causado pela força aplicada pela mola em . Faça um gráfico das três componentes escalares de e calcule o valor máximo absoluto de cada componente.

Primeiro vamos encontrar o vetor posição de . Ele tem uma coordenada fixa em m, e percorre um círculo de raio em com centro no ponto que é projeção de no plano . Podemos então escrever o vetor posição de dessa maneira:

Agora podemos achar o vetor e seu vetor unitário :

Agora que já temos o vetor unitário que representa a direção e sentido da força, precisamos achar o módulo. O módulo da força elástica com uma deformação é . O comprimento normal da mola é em quando a mola está vertical, e é igual a m. O comprimento da mola em função de é dado por

Então a deformação é:

E então o módulo da força elástica será:

Agora já temos o vetor da força:

E conseguimos calcular o momento causado em :

Agora mostramos os gráficos das componentes e de :

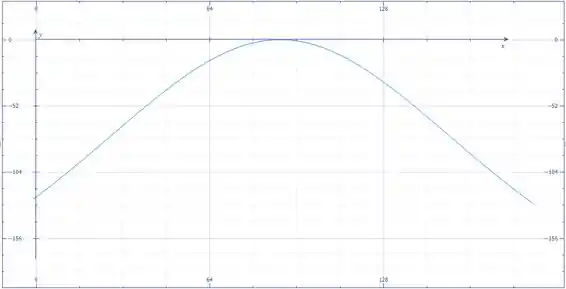
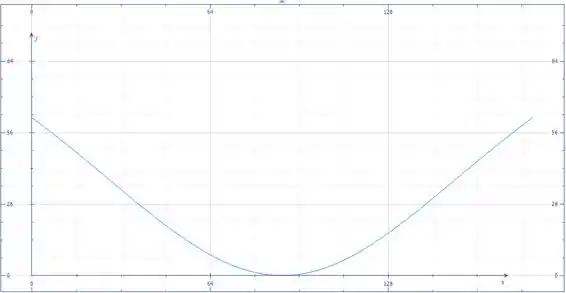
Podemos perceber que os máximos dos módulos das componentes e ocorrem em

E , onde temos e