Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 73

A chapa é feita de bronze Tobin, que escoa a σ e = 175   M P a . Pela teoria de falha da tensão de cisalhamento máxima, determine a tensão de tração máxima σ x que pode ser aplicada à chapa, se também for aplicada uma tensão de tração σ y = 0,75 σ x .

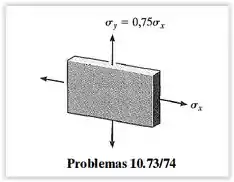
Passo 1

Oi, pessoal! Tudo bem com vocês?

O enunciado pede que determinemos a tensão de tração máxima σ x que pode ser aplicada à chapa, se também for aplicada uma tensão de tração σ y . Nos fornece:

σ e = 175   M P a

σ x

σ y = 0,75 σ x

τ x y = 0

Ele quer que a gente use a teoria de falha da tensão de cisalhamento máxima. Para isso, vamos precisar começar caculando a tensões principais, belezinha? Bora!

Passo 2

Vamos começar substituindo as tensões na equação das tensões principais:

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

Substituindo, temos:

σ 1,2 = σ x + 0,75 σ x 2 ± σ x - 0,75 σ x 2 2 + 0

σ 1,2 = 0,875 σ x ± 0,125 σ x

σ 1 = σ x

σ 2 = 0,75 σ x

Passo 3

Com as tensões principais em mãos, a gente pode escolher o caso que temos do critério usado. Já que as duas tensões principais tem o mesmo sinal, o caso do critério que a gente vai usar é

σ 1 = σ e

σ 2 = σ e

Aí o próximo passo é determinar a tensão de tração máxima de acordo com essa teoria da tensão de cisalhamento máxima.

Substituindo σ 1 :

σ 1 = σ e

σ x = 175   M P a

σ x = 175   M P a

Substituindo σ 2 :

σ 2 = σ e

0,75 σ x = 175   M P a

σ x = 233,333   M P a

Portanto, achamos dois possíveis resultados para σ x . Aí a gente lembra que sempre que falamos de tensão máxima permitida, escolhemos o menor valor encotrado, então:

σ x = 175   M P a

Resposta

σ x = 175   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 10.83 usando a teoria da tensão de cisalhamento máxima.
Se uma peça máquina for feita de titânio (Ti-6A1-4v) e um ponto crítico no material tiver as tensões principais σ 1 e σ 2 = σ 1 0,5 , determine o valor de σ 1 que provocará escoamento de acordo com (a
O estado de tensão que age em um ponto crítico sobre uma chave de porca é mostrado na figura. Determine a menor tensão de escoamento para o aço que poderia ser selecionado para a fabricação da ferrame
O pequeno cilindro de concreto com diâmetro de 50 mm está sujeito a um torque de 500 N.m e a uma força de compressão axial de 2 kN. Determine se ele falhará de acordo com a teoria da tensão normal máx
Um vaso de pressão esférico de parede fina tem raio interno r e espessura t e está sujeito a uma pressão interna p . Se as constantes do material forem E e v , determine a deformação na direção circun