Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 96
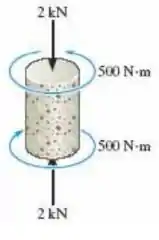
O pequeno cilindro de concreto com diâmetro de 50 mm está sujeito a um torque de 500 N.m e a uma força de compressão axial de 2 kN. Determine se ele falhará de acordo com a teoria da tensão normal máxima. O limite de resistência do concreto é
Passo 1
Primeiro, vamos determinar as tensões:
Logo, as tensões principais serão dadas por:
Substituindo os dados e fazendo a conta, teremos:
Como podemos ver, as duas tensões são menor que a tensão máxima admissível, logo o cilindro não falhará.
Resposta
O cilindro não falhará.
Exercícios de Livros Relacionados
O elemento está sujeito às tensões mostradas na Figura. Se σe = 350 MPa, determine o fator de segurança para essa carga com base na (a) teoria da tensão de cisalhamento máxima e (b) teoria da energia
Deduza uma expressão para um torque equivalente M e que, se aplicado sozinho a uma barra maciça de seção transversal circular, provocaria a mesma energia de distorção que a aplicação combinada de um m
O resultado do cálculo das cargas internas em uma seção crítica ao longo do eixo de acionamento de aço de um navio são um torque de 3,45 kN.m, um momento fletor de 2,25 kN.m e uma propulsão axial de 1
As componentes do estado plano de tensão em um ponto crítico sobre uma carcaça fina de aço são mostradas na figura. Determine se ocorre falha (escoamento) com base na teoria da energia de distorção má
As componentes de deformação no ponto A sobre a carcaça são ∈ x = 250 × 10 - 6 , ∈ y = 400 × 10 - 6 ,γ x y = 275 × 10 - 6 ,∈ z = 0 . Determine (a) as deformações principais em A, (b)a deformação por c