Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 94
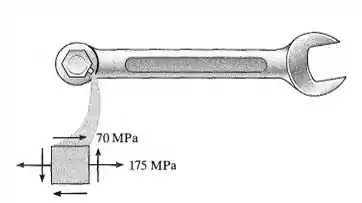
O estado de tensão que age em um ponto crítico sobre uma chave de porca é mostrado na figura. Determine a menor tensão de escoamento para o aço que poderia ser selecionado para a fabricação da ferramenta com base na teoria da energia de distorção máxima.
Passo 1
Primeiramente, sabemos que:
Logo, as tensões principais serão dadas por:
Substituindo os dados e fazendo a conta, teremos:
Passo 2
Agora, podemos utilizar a equação para calcular a tensão máxima:
Substituindo-se os dados obtidos e resolvendo a expressão, ficamos com:
Resposta
Exercícios de Livros Relacionados
A chapa é feita de bronze Tobin, que escoa a σ e=175M P a . Pela teoria da energia de distorção máxima, determine a tensão de tração σx que pode ser aplicada à chapa, se também for aplicada uma tensão
Uma liga de alumínio 6061- T6 deve ser usada para fabricar um eixo de acionamento maciço que transmite 33 kW a 2.400 rev/min. Usando um fator de segurança de 2 para o escoamento, determine o menor diâ
Uma liga de alumínio deve ser usada para fabricar um eixo de acionamento que transmite 20 kW a 1.500r e v / m i n .Usando um fator de segurança de 2.5 para escoamento, determine o menor diâmetro do ei
Uma barra com área de seção transversal quadrada é feita de um material cuja tensão de escoamento é σ e=840 M P a . Se a barra for submetida a um momento fletor de 10k N . m , determine o tamanho exig
As componentes do estado plano de tensão em um ponto crítico sobre uma carcaça fina de aço são mostradas na figura. Determine se ocorre falha (escoamento) com base na teoria da tensão de cisalhamento