Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 24

A chapa retangular é submetida à deformação mostrada pelas linhas tracejadas. Determine as deformações normais médias ao longo da diagonal AC e do lado AB.

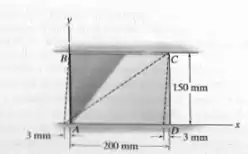
Passo 1

Falaa, meu querido! A fórmulinha da deformação normal média ao longo de um segmento de comprimento inicial é:

Precisamos então achar os comprimentos desses segmentos (final e inicial) onde ele pediu a deformação e jogar na fórmulinha, ok?

Para facilitar, a gente pode deixar aqui um esqueminha do que aconteceu. Para a diagonal :

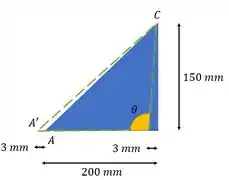
E para o lado :

O tracejado é a situação depois da deformação. Vamos achar nossos segmentos agora!

Passo 2

Vamos achar os comprimentos usando Pitágoras.

Para , temos que no começo o comprimento era e depois passou a valer:

Agora, para , o comprimento incial era:

E o final fica:

Passo 3

Podemos, com os dados calculados, obter as deformações:

-4

-3

Resposta

-4

-3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6.120 a 6.123 Para o dado estado plano de deformações usar o círculo de Mohr para determinar o estado de deformação associado aos eixos x'e y’, que foram girados de um ângulo θ , no sentido mostrado.

6.120 a 6.123 Para o dado estado plano de deformações usar o círculo de Mohr para determinar o estado de deformação associado aos eixos x'e y’, que foram girados de um ângulo θ , no sentido mostrado.

6.124 a 6.127 Para o estado plalno de deformação, usar o círculo de Mohr para determinar: (a ) a orientação e a intensidade das deformações específicas normais principais;(b) a máxima deformação espec

6.124 a 6.127 Para o estado plalno de deformação, usar o círculo de Mohr para determinar: (a ) a orientação e a intensidade das deformações específicas normais principais;(b) a máxima deformação espec

6.120 a 6.123 Para o dado estado plano de deformações usar o círculo de Mohr para determinar o estado de deformação associado aos eixos x'e y’, que foram girados de um ângulo θ , no sentido mostrado.