Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 29
O bloco é deformado até a posição mostrada pelas linhas tracejadas. Determine a deformação por cisalhamento nos cantos C e D.
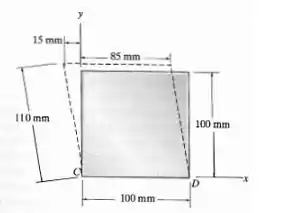
Passo 1
Fala aíí galera tudo bemmm? Sempre quando um material é submetido a uma tensão, ocorre algum tipo de deformação, como vocês podem ver alí embaixo.
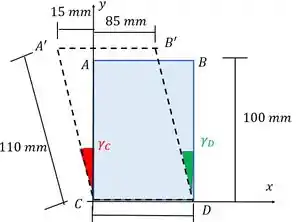
O que ele quer é a deformação de cisalhamento nos vértices e . Essa deformação é a diferença angular entre o ângulo inicial no vértice menos o final (essa ordem e importante):
Percebe que nosso elemento era um retângulo e depois virou um paralelogramo. Isso diz que o lado e são paralelos e fazem o mesmo ângulo com a vertical. Por isso vemos que
Mas percebe também que o ângulo em (entre ) no elemento inicial era de . Mas depois o ângulo entre e fica menor. Ou seja, a diferença entre ângulo inicial e final é positiva porque o ângulo final é menor que o inicial. Ou seja, é positivo.
Já no vértice acontece o inverso. O ângulo entre e é de , mas o ângulo entre e é maior que . Então o ângulo em aumenta, assim o valor de é negativo porque a diferença entre ângulo inicial e final é negativa.
Vamos seguir!
Passo 2
A gente já viu os sinais de e . Falta achar o valor desses ângulos, que vão ser iguais em módulo a . Para isso vamos usar trigonometria nesse triângulo que pode ser retirado da nossa figura:
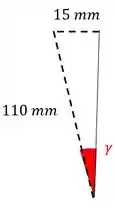
Por trigonometria, temos que
Para se encontrar em radianos vamos dividir esse cara por e multiplicar por :
Passo 3
Aí temos que
Mas como vimos que é negativo, temos
E vimos que é positivo, então: