Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 167
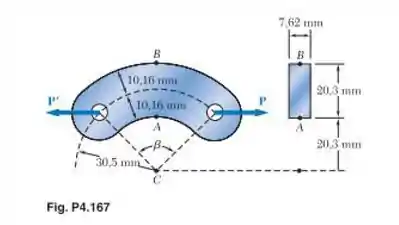
As chapas de ligação de aço com a seção transversal mostrada na figura estão disponíveis com diferentes ângulos centrais . Sabendo que a tensão admissível é de 82,7 MPa, determine a maior força P que pode ser aplicada a uma chapa de ligação para a qual .
Passo 1
Tá legal! Para começar esse exercício, precisamos calcular o centroide da seção dada. Para essa geometria, temos que o centroide se localiza em:
Sendo o raio médio e o ângulo de abertura. Dessa forma, substituindo os valores conhecidos para o nosso caso, teremos:
Agora vamos calcular o valor da área da seção transversal dessa seção, então teremos:
Agora, conforme vimos da Fig. 4.61 dessa seção, para a seção retangular de uma barra curvada, podemos encontrar o raio de superfície neutra através de:
Onde é o raio externo e é o raio interno. Dessa forma, substituindo os valores conhecidos para essa equação, chegamos em:
Passo 2
Agora vamos calcular a excentricidade, que é a distância entre o centroide e o eixo neutro da seção transversal, dessa forma, teremos:
Substituindo os valores conhecidos, teremos:
Agora podemos encontrar a tensão no ponto A (que será o ponto de maior tensão) através da equação 4.71, somado a parcela da força exercida por P, então teremos:
Sabendo que podemos escrever o momento gerado por em função do centroide da seção encontrado lá no passo 1, teremos:
Isolando P dessa equação, chegaremos na seguinte expressão:
Substituindo os valores conhecidos, chegamos na maior força P admissível: