Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 118

O cilindro hidráulico D se estende com uma velocidade v B = 1,2   m / s e uma aceleração a B = 0,45   m / s 2 . Determine a aceleração de C no instante mostrado.

Passo 1

Começaremos o exercício analisando o centro de velocidade instantâneo conforme a figura a seguir e a sua distância até o ponto B:

r B / C I = 0,6 c o s 30 ° → r B \ C I = 0,52   m

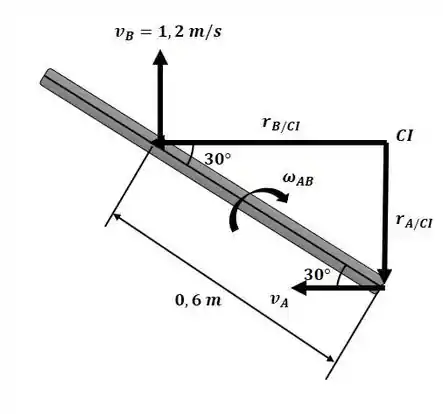
Sendo assim, podemos encontrar a velocidade angular do braço AB:

ω A B = v B r B / C I = 1,2 0,52 → ω A B = 2,308   r a d / s

Passo 2

Agora podemos aplicar a equação da aceleração para o sistema entre os pontos A e B com o auxílio do diagrama a seguir:

a → A = a → B + α A B × r → A / B - ω A B 2 r → A / B

- a A i → = 0,45 j → + - α A B k → × 0,52 i → - 0,3 j → - 2,308 2 ( 0,52 i → - 0,3 j → )

- a A i → = - α A B + 2,77 i → + ( 2,05 - 0,52 α A B ) j →

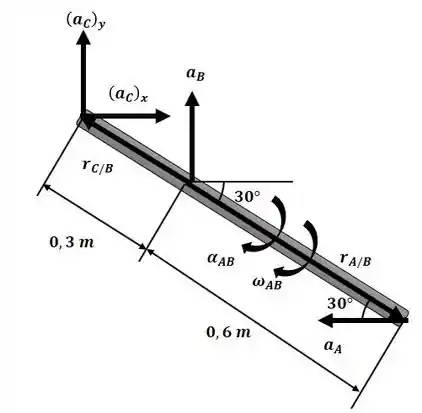
Agora igualando as componentes nas direções i e j, temos:

- a A = - α A B + 2,77

Essa será nossa equação 1.

0 = 2,05 - 0,52 α A B → α A B = 3,94   r a d / s 2

Substituindo esse valor na equação 1:

- a A = - 3,94 + 2,77 → a A = 6,71   m / s 2

Passo 3

Agora iremos aplicar a equação da aceleração entre os pontos B e C, ainda com o auxílio do diagrama apresentado no passo 2:

a → C = a → B + α A B × r → C / B - ω A B 2 r → C / B

a C x i → + a C y j → = 0,45 j → + - 3,94 k → × - 0,3 c o s 30 ° i → + 0,3 s e n 30 ° j → - 2,308 2 ( - 0,3 c o s 30 ° i → + 0,3 s e n 30 ° j → )

a C x i → + a C y j → = 0,793 i → + 0,675 j →

Igualando as componentes i e j temos:

a C x = 0,793   m / s 2

a C y = 0,675   m / s 2  

Sendo assim, o módulo de C é dado por:

a C = a C x 2 + a C y 2 = 0,793 2 + 0,675 2

a C = 1,04   m / s 2

E a direção é dada por:

θ = t g - 1 a C x a C y = t g - 1 0,675 0,793 → θ = 40,4 °

Resposta

a C = 1,04   m / s 2

θ = 40,4 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.160. No instante mostrado na figura, o comprimento da lança AB está sendo diminuído a uma taxa constante de 0,2 m/s e a lança está sendo baixada a uma taxa constante de 0,08 rad /s. Determine (a) a
15.161. No instante mostrado na figura, o comprimento da lança AB está sendo aumentado a uma taxa constante de 0,2 m/s e a lança está sendo baixada a uma taxa constante de 0,08 rad /s. Determine (a) a
A placa retangular mostrada na figura gira à taxa constante ω 2 = 12r a d / s em relação ao braço A E , que, por sua vez, gira à taxa constante ω 1 = 9r a d / s em torno do eixo Z . Para a posição mos
Resolva o Problema 15.222, considerando que, no instante mostrado, a velocidade angular ω 1 da placa de 10r a d / s está decrescendo a uma taxa de 25r a d / s 2 , enquanto a velocidade relativa u do p
Usando o método da Seção 15.14 , resolva o Problema 15.19 2 .