Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 146

O disco rola sem deslizar e, em um dado instante, tem o movimento angular mostrado. Determine a velocidade angular e a aceleração angular do membro com ranhura BC nesse instante. O pino em A está fixo ao disco.

Passo 1

Começaremos o exercício definindo nosso eixo xyz de referência conforme a figura a seguir:

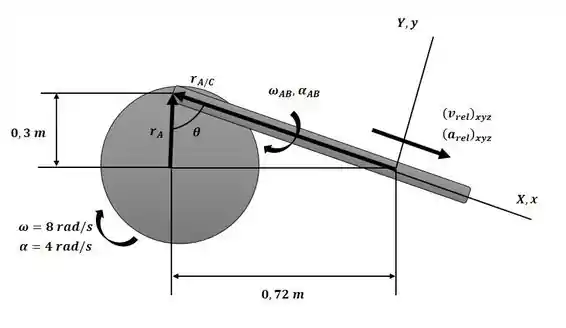
Sendo assim, temos:

v → C = a → C = 0

ω A B = - ω A B k →

ω ˙ A B = - α A B k →

Agora, com base na geometria do esquema anterior, temos:

r A / C = 0,3 2 + 0,72 2 → r A / C = 0,78   m

θ = t g - 1 0,72 0,3 → θ = 67,38 °

Para o movimento em torno do ponto A, temos:

r → A / C = - 0,78 i →   m

v → r e l x y z = v r e l x y z i →

a → r e l x y z = a r e l x y z i →

Passo 2

Uma vez que a roda A gira em torno de um eixo fixo, podemos encontrar a velocidade no ponto A da seguinte forma:

v → A = ω × r → A

v → A = - 8 k → × ( - 0,3 c o s 67,38 ° i → + 0,3 s e n 67,38 ° j → )

v → A = 2,215 i → + 0,923 j →   m / s

Podemos também calcular a aceleração no ponto A:

a → A = α × r → A - ω 2 r → A

a → A = - 4 k → × - 0,3 c o s 67,38 ° i → + 0,3 s e n 67,38 ° j → - 8 2 ( - 0,3 c o s 67,38 ° i → + 0,3 s e n 67,38 ° j → )

a → A = 8,492 i → - 17,262 j →   m / s 2

Agora iremos aplicar a equação da velocidade relativa para os pontos A e C:

v → A = v → C + ω A B × r → A / C + v r e l x y z

2,215 i → + 0,923 j → = 0 + - ω A B k → × - 0,78 i → + v r e l x y z i →

2,215 i → + 0,923 j → = v r e l x y z i → + 0,78 ω A B j →

Igualando as componentes i e j, temos:

v r e l x y z = 2,215   m / s

0,923 = 0,78 ω A B → ω A B = 1,18   r a d / s

Passo 3

Agora podemos aplicar a equação da aceleração relativa para o sistema:

a → A = a → B + ω ˙ A B × r → A / C + ω A B × ω A B × r → A / B + 2 ω A B × v r e l x y z + a r e l x y z

8,492 i → - 17,262 j → = 0 + - α A B k → × - 0,78 i → + - 1,183 k → × - 1,183 k → × - 0,78 i → + 2 - 1,183 k → × 2,215 i → + a r e l x y z i →

8,492 i → - 17,262 j → = a r e l x y z + 1,092 i → + ( 0,78 α A B - 5,244 ) j →

Igualando a componente j, temos:

- 17,262 = 0,78 α A B - 5,244 → α A B = - 15,41   r a d / s 2

Resposta

ω A B = 1,18   r a d / s

α A B = 15,41   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que, no instante mostrado, a manivela BC tem uma velocidade angular constante de 45 rpm no sentido horário, determine a aceleração (a) do Ponto A, (h) do Ponto D.
Resolva o problema 15.252 assumindo que o prato F está movendo para a direita com velocidade constante de 9 in/s
A água flui através de um tubo curvo AB que gira com uma velocidade angular constante no sentido horário de 90 rpm. Se a velocidade da água em relação ao tubo for 8 m / s, determine a aceleração total
A haste BC de 24 pol de comprimento é conectada por articulações esféricas a um braço rotativo AB e a um colar C que desliza na haste fixa DE. Sabendo que o comprimento do braço AB é de 4 pol e que el
A haste AB de comprimento 125 mm é fixada a uma haste vertical que gira em torno do eixo y a uma taxa constante ω 1 = 5 r a d / s . Sabendo que o ângulo formado pela haste AB e a vertical está aumenta