Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 111
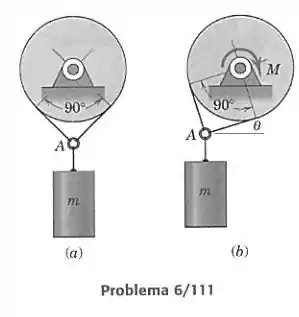
O cilindro de massa está preso ao anel , que está suspenso pelo cabo que passa sobre a polia, como mostrado na parte da figura. Um momento aplicado à polia a faz girar até que ocorre deslizamento do cabo na polia na posição , como mostrado na parte da figura. Calcule o coeficiente de atrito entre o cabo e a polia.
Passo 1
No limiar do deslizamento, quando , podemos dizer que o canbo ainda está em equilíbrio em torno da polia. A fórmula para o equilíbrio de uma corda enrolada em torno de uma superfície é dada por:
Sendo e as trações maior e menor nas extremidades do cabo, o ângulo total de enrolamento do cabo e o coeficiente de atrito entre o cabo e a superfície. Através das equações de equilíbrio para o anel , devemos ser capazes de encontrar a relação entre as trações e , e assim usaremos a fórmula para achar .
Passo 2
Vamos fazer o diagrama de corpo livre do anel , se atentando aos ângulos de inclinação das extremidades do cabo:
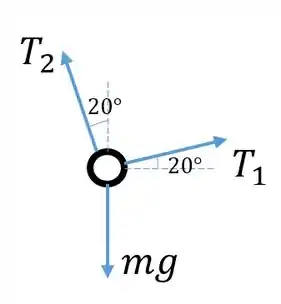
Achamos a relação entre e através da soma das forças horizontais, já que o peso não aparece:
Passo 3
Agora que temos a razão , aplicamos na fórmula:
O ângulo é três quartos de volta, então: