Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 94
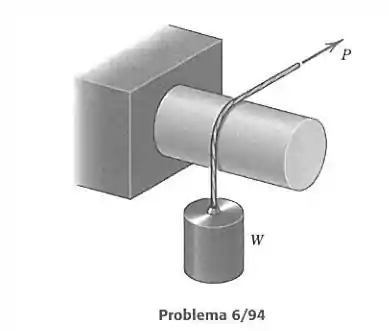
Determine a força necessária para levantar e abaixar o cilindro de peso a uma velocidade constante baixa. O coeficiente de atrito entre a corda e o eixo fixo vale 0,4.
Passo 1
Como queremos que o movimento da corda seja constante, podemos dizer que a corda estará em equilíbrio. A fórmula para o equilíbrio da corda enrolada no cilindro é dada por:
Sendo e as trações maior e menor nas extremidades, o coeficiente de atrito entre a corda e o eixo e o ângulo total de giro da corda. Através dessa fórmula, seremos capazes de achar nos dois casos.
Passo 2
- Para levantar, a força maior deve ser , então e . Além disso, o ângulo total de giro é o ângulo de um quarto de circunferência:
- Para abaixar o peso, temos e . Então:
Então jogamos na fórmula:
Passando para a forma exponencial:
Passo 3
Resposta
Exercícios de Livros Relacionados
O caixote de 10 Mg é abaixado para uma câmara de armazenamento subterrânea em um elevador de dois parafusos projetado como mostrado. Cada parafuso tem uma massa de 0,9 Mg, um diâmetro médio de 120 mm
A figura mostra uma transmissão de vários discos projetada para uso marítimo. Os discos de potência A são encaixados em uma canaleta no eixo, mas têm que girar com ele. Os discos C atuam sobre a estru
Um mancal radial para um eixo sob uma carga axial L é projetado como um copo esférico parcial de raio r . Se a pressão entre as superfícies do mancal em qualquer ponto varia de acordo com p = p 0 cos
Determine a expressão para o torque M necessário para girar o eixo cuja pressão axial L é sustentada por um mancal cômico. O coeficiente de atrito é μ , e a pressão no mancal é constante.
Os blocos de 10 kg e de 25 kg estão presos por uma corda pendurada sobre a superfície curva fixa. Se o sistema está no limiar de escorregar, calcule o coeficiente de atrito entre a corda e a superfíci