Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 138
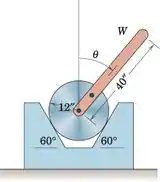
O cilindro pesa 80 lb e a barra esguia uniforme anexada tem um peso desconhecido W. A unidade permanece em equilíbrio estático para valores do ângulo variando até 45, mas desliza se exceder 45. Se o coeficiente de atrito estático for conhecido como sendo 0,30, determine C.
Passo 1
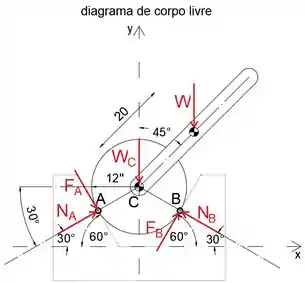
Primeiro, vamos isolar o diagrama de corpo livre do cilindro com seu peso WC, peso da barra fina W e as forças de reação em A e B atuando nele
Como o cilindro está prestes a escorregar a = 45º, podemos assumir que o escorregamento ocorre tanto em A quanto em B simultaneamente, então podemos escrever as forças de atrito FA e FB às
Passo 2
Podemos calcular a distância AB do triângulo ABC usando a regra do cosseno
Uma vez que tanto AC quanto BC fazem com o ângulo horizontal de 30, podemos escrever o ângulo ACB como
Substituiremos , e ACB por seus valores na expressão (1)
Passo 3
Ao igualar a soma dos momentos sobre o ponto A a zero, podemos escrever a força de reação normal NB como função do peso W
Substituiremos WC e por seus valores e FB por 0,30NB
A partir daqui, podemos expressar NB como
Passo 4
Ao igualar a soma dos momentos sobre o ponto C a zero, podemos escrever a força de reação normal NA como função do peso W
Podemos substituir FA por 0,30NA e FB por 0,30NB
A seguir, podemos substituir NB pela expressão (1)
A partir daqui, podemos expressar NA como
Passo 5
Finalmente, ao igualar a soma das forças na direção x a zero, podemos escrever a equação onde o peso W é a única incógnita
Primeiro vamos substituir FA por 0,30NA e FB por 0,30NB
A seguir, substituiremos NA e NB pelas expressões (2) e (1), respectivamente