Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 143
Trace a força P necessária para começar a mover a caixa de 100 kg subindo a inclinação 10, começando do repouso em vários valores de x de zero a 10 m. Determine o menor valor possível de P e o valor correspondente de x.
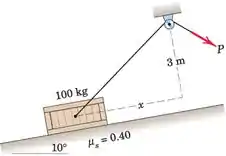
Passo 1
O enunciado pede que a gente determine o menor valor possível de P e o valor correspondente de x.
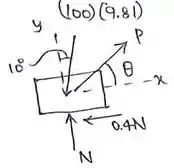
Passo 2
Ao eliminar N, obtemos
para valor estacionário
Resposta
Exercícios de Livros Relacionados
Determine a força de atrito na caixa de 40k g e a força normal resultante em sua posição x , medida a partir do ponto A , se a força é P=300N . Considere μ s = 0,5 e μ k = 0,2 .
O gancho por atrito é composto de uma estrutura fixa e de um cilindro de peso desprezível. Um pedaço de papel é colocado entre a parede e o cilindro. Se θ=20 º º, determine o menor coeficiente de atri
O disco tem peso W e encontra-se em um plano que possui coeficiente de atrito estático m. Determine a maior altura h à qual o plano pode ser elevado sem fazer com que o disco deslize.
O semicilindro homogêneo tem massa de 20k g e centro de massa em G. Se a força P é aplicada na borda, e r=300m m , determine o ângulo θ quando o semicilindro está na iminência de deslizamento. O coefi
Determine o maior ângulo θ de modo que a escada não deslize quando um homem de 75 kg estiver na posição mostrada. A superfície é um tanto escorregadia, onde o coeficiente de atrito estático em A e