Se os cilindros C e D pesam cada um 5k N , determine a flecha máxima h e o comprimento do cabo entre as polias lisas em A e B . A viga tem um peso por unidade de comprimento de 2k N / m .

Enunciado

O problema quer que a gente encontre a flecha máxima e o comprimento do cabo entre as polias lisas e .

Vamos começar observando um pouco o problema, assim a gente pode fazer um diagrama de corpo livre, assim:

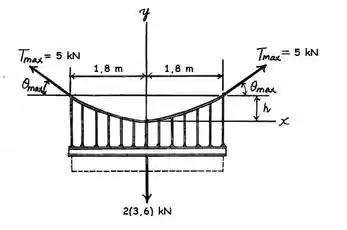
Agora, vamos analisar as forças no eixo , lembrando que o corpo está em equilíbrio:

E encontramos o ângulo máximo:

Agora, a gente pode obter:

Nós notamos que na figura do problema, é o ponto mais baixo do cabo, vamos pegar a segunda derivada da equação do cabo, logo:

E integrando isso:

Vamos encontrar , pra isso a gente usa a condição inicial, de que na origem, e então:

Logo é igual a .

Ficamos com:

Integramos mais uma vez para chegamos na função não derivada:

Aplicamos a condição inicial também para descobrirmos :

Encontramos que também é nulo. Então, ficamos com a função do cabo como sendo:

Agora, descobrir , usando e , que vimos no problema, aplicando na função, fica:

Por ultimo, vamos ter que usar uma integral para calular o comprimento do cabo, então vamos calcular equação diferencial do comprimento:

Lembra, que a gente já tem essa primeira derivada, vamos substituir ela, e fica:

Vamos integram agora para descobrir o comprimento total:

Obs.: A gente vai calcular a integral apenas para a parte positiva e multiplicar por .

Resolvendo essa integral, obtemos como resposta: