Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 100
O cabo suporta a carga distribuida uniforme de . Determine a tração no cabo em cada apoio e .
Passo 1
O problema quer que a gente encontre a tração em cada apoio.
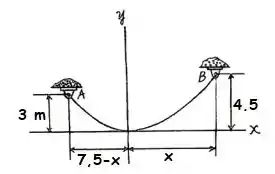
Vamos começar usando a equação do cabo, que a gente pode encontrar no livro no exemplo 7-12:
Aplicamos os valores em cada apoio:
Então:
Obtemos:
Resolvendo essa equação encontramos:
Mas com o cabo só se extende no eixo até , então o resultado que serve pra gente é:
Passo 2
Então, agora vamos calcular a força com a mesma equação:
Vamos analisar :
Derivando e lembrando que a derivada é a tangente do ângulo:
Então:
Agora sim, calculamos a tração:
Passo 3
Agora, faremos o mesmo no :
Derivando e lembrando que a derivada é a tangente do ângulo:
Então:
Agora sim, calculamos a tração:
Resposta
Exercícios de Livros Relacionados
Determine a força normal interna, o esforço cortante e o momento atuando no ponto C , e também no ponto D , que está localizado à direita do apoio de rolete em B .
Determine a força normal interna, o esforço cortante e o momento nos pontos C e D da viga simplesmente apoiada. O ponto D está localizado à esquerda da força de 5k N .
Determine a distância a em termos da dimensão L da viga entre os apoios A e B simetricamente posicionados de modo que o momento interno no centro da viga seja zero.
Determine a força normal interna, o esforço cortante e o momento nos pontos D e E nos dois membros.
Determine a razão de a / b para a qual o esforço cortante será zero no ponto intermediário C da viga com dupla extremidade em balanço.