Cinco tiras de metal, cada uma com 40 mm de largura, são firmemente unidas, de maneira a formar a viga composta mostrada. Os módulos de elasticidade são de para o aço, para o latão e para o alumínio. Sabendo-se que a viga é encurvada em torno de um eixo horizontal por um momento , determinar a máxima tensão:
- No aluminio;

Passo 1
Quando temos mais de um material na nossa barra precisamos converter todos ela para um deles para facilitar o nosso cálculo.
Sabemos que o nosso fator a ser calculado é dado por:
Vamos então fazer o seguinte, vamos manter como intacto o Aço, e vamos transformar em aço o latão e o alumínio, sendo assim vamos ter dois fatores de transformação, sendo assim teremos que:
E como temos duas mudanças, precisamos modificar a largura das chapas de latão e de alumínio, e como elas foram as transformadas, então o aço vai se manter, e o latão e alumínio vão ser modificados:
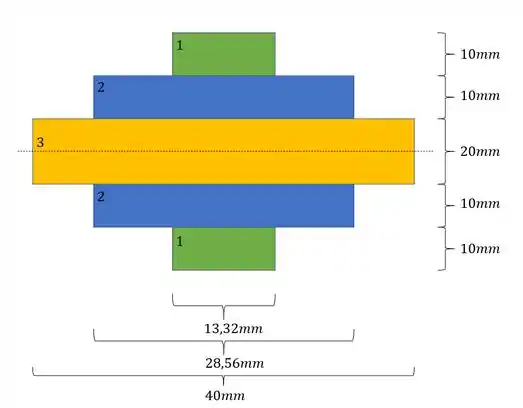
Sendo assim a nova seção é dada por:
Nosso objetivo é determinar as tensões, e a fórmula que calcula a tensão na estrutura intacta, é dada por:
E a fórmula para calcular as tensões nas barras que foram transformadas é dada por:
Ou seja, temos que tomar cuidado de usarmos o coeficiente de transformação correto, na barra correta.
Agora já podemos determinar o momento de inércia e o y da nossa fórmula.
Passo 2
Como já temos a LN, podemos determinar o momento de inércia, e com isso vamos seguir o seguinte passo a passo.
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Área das regiões
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
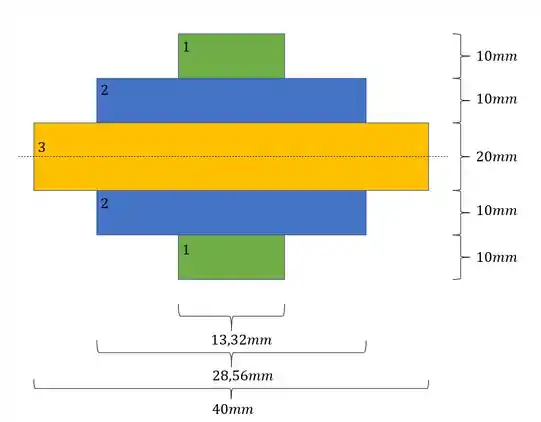
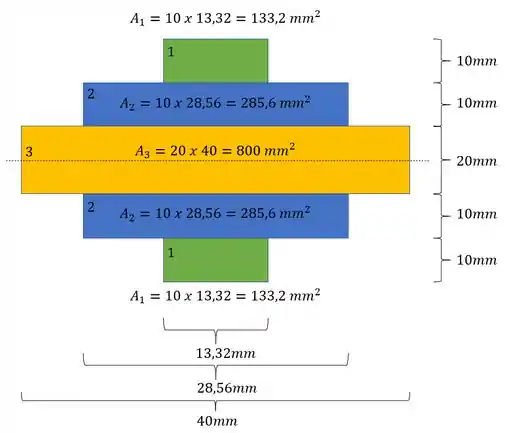

- positivo e negativo

Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Sendo assim teremos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 3
Pelo enunciado, o nosso objetivo é determinar a máxima tensão no aluminio, logo, precisamos determinar y apenas do aluminio, e lembrando que ele é a parcela transformada, ou seja, possui fator de transformação multiplicando a tensão, sendo assim teremos que:
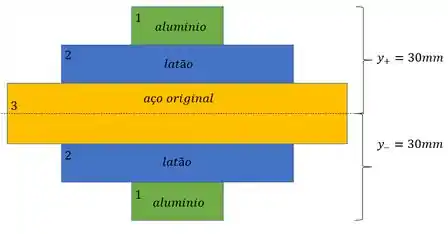
Calculando primeiro o latão:
Substituindo, teremos que: