Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 8.Problemas fundamentais - Ex. 4
Se o coeficiente de atrito estático nos pontos de contato e for , determine a força máxima que pode ser aplicada sem fazer com que o carretel de se mova.
Passo 1
Fala ai galerinha bonita, tudo beleza?
Saca só, nesse exercício aqui a gente quer encontrar o valor máximo de de tal forma que o carretel não se mova. Para isso, tomemos o seguinte diagrama de forças, lembrando que a força de atrito se comporta contra a tendência do movimento
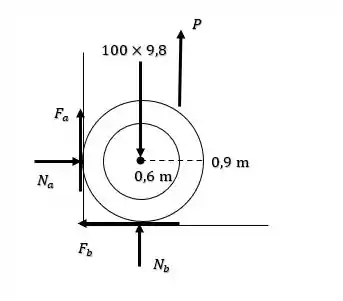
Utilizando a equação de equilíbrio para o eixo vamos ter:
Agora, para o eixo :
Calculando, também, o momento para o centro das nossas esferas vamos obter:
Passo 2
Iradoso, e como as forças e são forças de atrito, teremos que:
Onde o coeficiente de atrito é dado como , sendo assim:
Então podemos reescrever a equação , tal que:
E também podemos reescrever a equação como:
E por último, podemos reescrever a equação :
Passo 3
Show de bolinhas, agora a gente pode substituir a equação na equação , tal que:
Isolando :
E como vimos que , então:
E a malandragem é que agora a gente pode substituir e na equação , de modo que:
Isolando :
Portanto: