Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas - Ex. 19
Determine a tração desenvolvida em cada um dos fios usados para sustentar o candelabro de .
Passo 1
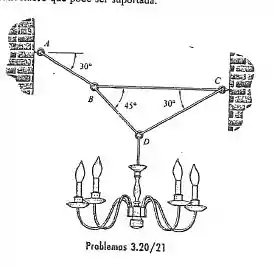
Fala galerinha do RespondeAí, bora fazer mais essa questão de mecânica? Saca so, o enunciado nos disse que um candelabro está suspenso através de cabos como na figura abaixo:
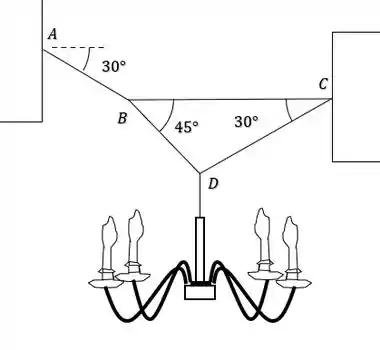
O enunciado nos diz que o sistema está em equilíbrio, e sabendo que o candelabro tem , ele nos pede para determinar todas as trações que ocorrem nos fios.
Mas calma lá, porque pensa aqui comigo, os pontos e , são pontos fixos presos na parede, então com toda certeza eles não vão se mexer nesse caso. Isso quer dizer que os únicos pontos que podem de fato interferir no equilíbrio do sistema, isso é, que podem se mexer, são os pontos e .
Ou seja, para toda essa situação estar em equiíbrio, precisamos que os pontos e estejam em equilíbrio também, logo o somatório das forças neles vai zerar.
Então, a gente pode analisar esses dois pontos através dessas equações e achar todas as trações nos cabos, belezinha? Bora lá então.
Passo 2
Vamos começar pelo ponto , porque a gente já tem uma das trações sobre ele: o peso do candelabro.
Então o Diagrama de Corpo Livre vai ficar assim:
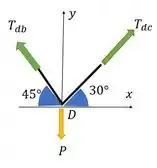
Precisamos então encontrar essas duas forças e .
Então no eixo , vamos obter que:
Já no eixo :
Agora ficou bonito, se a gente resolver esse sistema, vamos obter que:
Passo 3
Iradoso, agora vamos fazer a mesma coisa para o ponto , o diagrama de corpo livre é dado como:
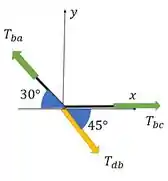
Mesma situação. Temos duas icógnitas e duas equações, então vai dar bom! A força amarelinha a gente achou no passo anterior.
Aí decompondo essas forças e usando as equações de equilíbrio para o eixo , teremos que:
E para o eixo :
Logo:
E susbituindo esse resultado na primeira equação, vamos obter que: