Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 12
Se um torque de for aplicado ao volante, determine a força que deverá ser desenvolvida no cilindro hidráulico para impedir que o volante gire. O coeficiente de atrito estático entre a pastilha de atrito em e o volante é .
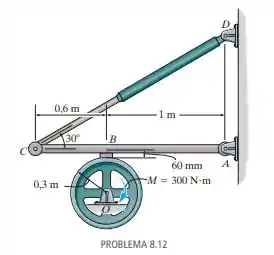
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Primeiramente, sabemos que a força de atrito deve gerar um momento maior que o de
Logo:
O momento gerado por ela é:
Portanto:
Para determinar a força em
Decompondo na direção de
Portanto, esta é a força pedida.
Resposta
Exercícios de Livros Relacionados
A barra esbelta uniforme tem um rolo ideal em sua extremidade superior A. Se o coeficiente de atrito estático em B for μ s =0,25 , determine o ângulo mínimo θ para o qual o equilíbrio é possível. Repi
Um binário M no sentido horário é aplicado ao cilindro circular, como mostrado. Determine o valor de M necessário para iniciar o movimento para as condições m B = 3k g , m C = 6k g , μ s B = 0,50 , μ
A roda de 100l b rola em seu eixo subindo a inclinação circular sob a ação do peso de 25l b preso a uma corda ao redor do aro. Determine o ângulo em que a roda para, supondo que o atrito seja suficien
Calcule a magnitude do binário M no sentido horário necessário para girar o cilindro de 50k g no bloco de suporte mostrado. O coeficiente de atrito cinético é 0,30 .
O bloco retangular homogêneo de massa m repousa sobre o plano inclinado que é articulado em torno de um eixo horizontal através de O . Se o coeficiente de atrito estático entre o bloco e o plano for μ