Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 95
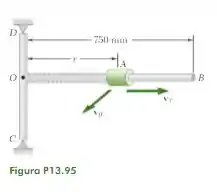
Um colar de está preso a uma mola de constante e comprimento indeformado de . O sistema é posto em movimento com , e . Desprezando a massa da barra e o efeito de atrito, determinar os componentes radial e transversal da velocidade do colar quando .
Passo 1
Oooi, pessoal! Tudo bem com vocês?
Nessa questão o nosso objetivo é encontrar os componentes radial e transversal da velocidade do colar quando . Primeiro vamos anotar os dados que são fornecidos.
Sabendo de tais dados, agora vamos calcular a deflexão da mola na posição inicial do colar. O problema nos diz que ele é posto em movimento com e . Observe que ele parte de uma posição na qual a mola está comprimida.
E, sendo e , temos que,
Passo 2
O problema pede que determinemos as componentes da velocidade do colar, quando , então esse é o nosso . Em metros,
Temos então que,
Passo 3
Vamos agora aplicar o princípio da conservação do momento angular.
Se você observar, o único valor que não temos ainda é a componente transversal da velocidade , que é um dos resultados solicitados no problema.
Isolando-a e substituindo os dados que já obtidos, temos:
Passo 4
O próximo passo é aplicar o princípio da conservação de energia: quando uma partícula se desloca sob a ação de forças conservativas, a soma da energia cinética e da energia potencial da partícula permanece constante. Assim, Eq. (13.24):
Agora, isolando e fazendo as substituições, obtemos:
Passo 5
Em posse de e de , podemos encontrar .