Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 67
A caixa tem massa de 150 kg e repousa em uma superfície para a qual os coeficientes de atrito estático e cinético são , respectivamente. Se o motor M fornece uma força no cabo N, onde t é dado em segundos, determine a potência de saída desenvolvida pelo motor quanto t=5s.
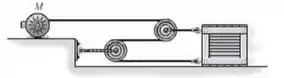
Passo 1
Fazendo o DCL para o sistema da figura, podemos montar as equações em relação ao eixo x e y.
I
Para o atrito estático, com o intuito de encontrar o momento do inicio do movimento do bloco:
Para o atrito cinético:
m/s2
Passo 2
Como foi obtido a equação da aceleração, podemos encontrar a velocidade integrando:
m/s
Passo 3
Para s, a força F será:
N
Devemos multiplicar a força por um fator de 3, devido a presença de duas polias, então a potência será:
Resposta
A potência será de 1.12 kW
Exercícios de Livros Relacionados
Um colar C de 1,2 kg pode deslizar sem atrito ao longo da haste horizontal. Ele está preso a três molas, cada uma de constante k = 400N / m e 150m m de comprimento indeformado. Sabendo que o colar é l
Uma força P é lentamente aplicada a uma placa que está presa a duas molas, causando uma deflexão x 0 . Para cada um dos casos mostrados na figura, deduza uma expressão para constante k e , em termos k
Um colar B de 5 kg pode deslizar sem atrito ao longo da haste horizontal e está em equilíbrio em A quando ele é puxado 125 mm para a direita e liberado. O comprimento indeformado de cada mola é 300 mm
Uma corda elástica é esticada entre dois pontos A e B , separados de 16 cm no mesmo plano horizontal. Quando esticada diretamente entre A e B , a tração na corda é de 10 N. A corda é, então, esticada
Uma mola é usada para parar um pacote de 50 kg que está se movendo para baixo numa inclinação de 20°. A mola tem constante k = 30 kN/m e é mantida por cabos de modo que está comprimida inicialmente de