Uma coluna de de comprimento efetivo é obtida pela conexão de quatro perfis laminados de aço com barras de travejamento,como indicado. Sabendo-se que e , determinar a carga centrada admissível para a coluna.
Passo 1
Então gurizada, vamos iniciar fazendo algumas conversões, para facilitar um pouco:
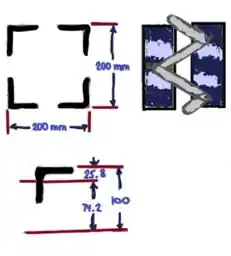
Agora, vamos a nossos cálculos:
Aço: