Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 71

A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a deflexão máxima da coluna e a tensão máxima na coluna.   E = 200 G P a ; σ y = 360 M P a .

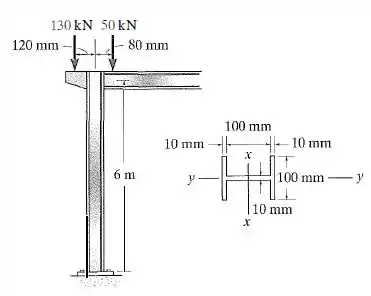
Passo 1

Primeiramente, vamos calcular os momentos de inércia e a área da seção:

I x = 2 100 × 10 3 12 + 100 × 10 × 55 2 + 10 × 100 3 12 = 6,9 × 10 6 m m 4

I y = 2 10 × 100 3 12 + 100 × 10 3 12 = 841666,667 m m 4

A = 2 100 × 10 + 100 × 10 = 3000 m m ²

Agora, devemos calcular alguns parâmetros:

r x = I x A = 47,958 m m

c = d 2 = 60 m m

e y = 64,44 m m

A deflexão máxima será dada por:

v m á x = e sec ⁡ P E A k L 2 - 1

Substituindo, teremos:

v m á x = 10,8 m m

Para a tensão máxima, a fórmula será:

σ m á x = P A ( 1 + e y c r x 2 sec ⁡ k L 2 r x P E A

Substituindo, teremos:

σ m á x = 178 M P a

Como a tensão é menor que a de escoamento, os dados são coerentes.

Resposta

v m á x = 10,8 m m

σ m á x = 178 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força centrada de 72 kN precisa ser suportada por uma coluna de alumínio conforme mostra a figura. Usando a liga de alumínio 6061-T6, determine a dimensão b mínima que pode ser usada.
Uma coluna com 6,4m de comprimento efetivo é obtida conectando quatro cantoneiras de aço L89 x 89 x 9,5mm com barras de travamento conforme mostrado. Utilizando método das tensões admissíveis, determi
Uma coluna com comprimento de flambagem de 6,4m é obtida ligando-se dois perfis U de aço U250 x 30 com barras de travejamento conforme mostra a figura. Usando o método da tensão admissível, determine
A coluna constituída de laminados colados mostrada na figura está livre no topo A e engastada na base B. Usando um tipo de madeira que tem uma tensão admissível ajustada a compressão paralela as fibra
Um membro comprimido de comprimento de flambagem igual a 2,3m é obtido conectando-se com parafusos duas cantoneiras de 127 x 7 x 12,7 conforme mostrado. Usando o método por tensões admissíveis, determ